Lokale Analyse des Quasiintegrals

Die charakteristische Eigenschaft eines Integrals der Bewegung ist seine Konstanz entlang von Trajektorien im Phasenraum. Bei einem formalen Integral der Bewegung ist dieses Verhalten im allgemeinen nicht zu erwarten, wie wir in Abschnitt 1.2.4 besprochen haben. Es ist keineswegs sichergestellt, daß die Potenzreihenentwicklung für das Integral, die wir als Resultat der Normalformtransformation erhalten, mit wachsendem Approximationsgrad $m$ konvergiert. Wenn das formale Integral $I_{\rm DFS}$ unabhängig von $\H$ und das System nichtintegrabel ist -- was in der Regel der Fall ist -- dann darf die normalisierende Transformation nicht konvergieren, denn dies stünde im Widerspruch zur Nichtintegrabilität. Mit anderen Worten: Das formale Integral stellt den Versuch dar, ein Integral zu approximieren, das gegebenenfalls gar nicht existiert. Trotzdem kann auch ein divergentes formales Integral die Situation im Phasenraum mit hoher Genauigkeit widerspiegeln [Mo68]. Wir werden diese Tatsache anhand von $I_{\rm BG}$ ausführlich belegen.

Eine weitere Komplikation ergibt sich dadurch, daß uns im Rahmen dieser Theorie nur Quasiintegrale zugänglich sind. Wir können die Transformation auf Normalform nur bis zu einem endlichen Grad $m_{\rm max}$ durchführen und erhalten dementsprechend prinzipiell nur eine Näherung des formalen Integrals. Dieser Umstand erschwert die Analyse des formalen Integrals, denn selbst wenn man für die Folge von Quasiintegralen $I^{(m)}$, $2\leq m\leq m_{\rm max}$ Konvergenz nachweisen kann, hat man im allgemeinen keine Möglichkeit, Aussagen auch für $m>m_{\rm max}$ zu machen. Divergenz für größere $m$ als $m_{\rm max}$ kann also nicht ad hoc ausgeschlossen werden.

Vor diesem Hintergrund führen wir eine neue Bezeichnungsweise ein, die für die Untersuchung der Konvergenzeigenschaften von $I^{(m)}$ nützlich ist: Wir beschränken den Begriff ,,Konvergenz`` auf den uns zugänglichen Wertebereich von $m$ und nennen ein Quasiintegral $I^{(m)}({\mbox{\protect\boldmath$z$}})$ konvergent an der Stelle ${\mbox{\protect\boldmath$z$}}$, wenn dort

$$\left\vert I^{(2m+2)}({\mbox{\protect\boldmath$z$}})-I^{(2m... ...vert \quad \mbox{f\uml {u}r} \quad 1<m<\frac{m_{\rm max}}{2}$$ (4.13)

gilt. Anderenfalls heißt $I^{(m)}({\mbox{\protect\boldmath$z$}})$ divergent. Bei dieser Definition haben wir berücksichtigt, daß $I^{(m)}$ eine gerade Funktion ist und wir ungerade Polynomgrade $m$ deshalb nicht einbeziehen müssen.

Wir untersuchen jetzt die Qualität des in Abschnitt 4.1.2 hergeleiteten Quasiintegrals $I_{\rm BG}^{(m)}$. Vorab erinnern wir daran, daß wir in Kapitel 3 die Nichtintegrabilität des Brown-Gabrielse-Systems nachgewiesen haben. Weil dieses autonome Hamilton-System zwei Freiheitsgrade der Bewegung hat und mit $H_{\rm BG}$ schon ein erstes Integral der Bewegung bekannt ist, kann kein zweites, von $H_{\rm BG}$ unabhängiges Integral existieren. Wenn das nach der DFS-Theorie berechnete formale Integral unabhängig von der Hamilton-Funktion ist, dann muß demnach $I_{\rm BG}$ bei allen Energien $E$ und für alle ${\mbox{\protect\boldmath$z$}}$ divergieren -- im gewöhnlichen Sinn des Begriffes Divergenz. Im Sinn von Gl. (4.25) ist aber immer noch Konvergenz des Quasiintegrals möglich. Wir zeigen im folgenden, daß sie bei bei niedrigen Energien die Regel ist und auch bei höheren Energien nicht ausgeschlossen werden kann.

Im ersten Schritt der Analyse von $I_{\rm BG}^{(m)}$ prüfen wir, inwieweit diese Polynome entlang den Lösungskurven der kanonischen Gleichungen (3.6) konstant sind. Das hierfür benutzte Verfahren wird beispielsweise auch in [DrFi79,St91] angewandt.

Das Quasiintegral $I_{\rm BG}^{(m)}$ ist eine Funktion der Phasenraumkoordinaten $\rho$, $z$, $p_\rho$ und $p_z$. Indem wir einen Punkt des Phasenraumes -- der Einfachheit halber betrachten wir nur Punkte ${\mbox{\protect\boldmath$s$}}=(z,p_z)^T$ aus der Poincaré-Fläche $\Sigma_E\subset{\bf R}^4$ -- als Startwert einer Trajektorie ansehen, diese durch numerische Integration berechnen und dann $I_{\rm BG}^{(m)}$ längs der Trajektorie auswerten, erhalten wir das Quasiintegral als Funktion der Zeit:

$$I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}}) := I_{\r... ...{(m)}\left(\Phi_t({\mbox{\protect\boldmath$s$}})\right) \quad.$$ (4.14)

In der Regel variiert $I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ für alle ${\mbox{\protect\boldmath$s$}}$ als Funktion der Zeit, denn selbst wenn $I_{\rm BG}$ ein (nicht nur formales) Integral der Bewegung ist, kann man erst im Grenzübergang $m\to\infty$ erwarten, daß das Quasiintegral $I_{\rm BG}^{(m)}$ konstant wird. Um so eher gehen wir auch im Fall der Nichtkonvergenz davon aus, daß $I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ zeitlich oszilliert. Divergenz im Sinn von Gl. (4.25) zeigt sich dann meistens dadurch, daß die Amplitude dieser Oszillationen mit $m$ anwächst. Es ist aber auch möglich, daß das Quasiintegral zunächst im Sinn von Gl. (4.25) konvergiert und erst für größere $m$ divergent wird.

In den Abbildungen 4.1 bis 4.6 haben wir jeweils das Quasiintegral der Brown-Gabrielse-Magnetflasche als Funktion der Zeit in verschiedenen Approximationen ( $m=2,4,\dots,14$) dargestellt; dabei wurden die Energie $E$ und der Startwert ${\mbox{\protect\boldmath$s$}}$ systematisch variiert. Offensichtlich hängen die Konvergenzeigenschaften der Quasiintegrale empfindlich sowohl von der Energie (also dem Systemparameter, dessen Erhöhung zu sich ausbreitendem Chaos führt), als auch von dem Startpunkt ${\mbox{\protect\boldmath$s$}}$ der betrachteten Trajektorie ab. Diese Tatsache steht in enger Analogie zu den Eigenschaften der Poincaré-Abbildung, die ebenfalls in Abhängigkeit von $E$ und ${\mbox{\protect\boldmath$s$}}$ reguläre oder chaotische Dynamik zeigt, wie man den Poincaré-Schnitten in Abschnitt 3.2.2 entnehmen kann.

Die Abbildungen 4.1, 4.2 und 4.3 zeigen, bei jeweils gleicher Energie $E=0.01$, schnelle Konvergenz des Quasiintegrals, langsame Konvergenz beziehungsweise Divergenz von $I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}})$. Bei der gleichen Energie ergibt sich demnach ein ganz unterschiedliches Konvergenzverhalten, je nachdem, wie weit der Startpunkt der Trajektorie vom Ursprung der Poincaré-Fläche entfernt ist.

Dieser Effekt läßt sich leicht aus dem lokalen Charakter des formalen Integrals erklären. Die Konvergenz ist um so besser, je näher der betrachtete Punkt am Entwicklungspunkt, dem Ursprung des Phasenraumes, liegt. Wir können diese Erklärung anhand der Abbildungen 4.1 bis 4.3 bestätigen, wenn wir den Verlauf der Kurven $I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ genauer betrachten. Bei der Oszillation des Quasiintegrals handelt es sich offensichtlich um die Überlagerung einer hoch- und einer niederfrequenten Schwingung. Der Vergleich mit den Daten der numerisch integrierten Trajektorie zeigt, daß die höherfrequente Oszillation in $\rho$-Richtung stattfindet, während der niederfrequente Anteil die Bewegung in $z$-Richtung widerspiegelt -- im Einklang mit den Überlegungen in Abschnitt 3.2.1. Weil der zugängliche Teil des Phasenraumes entlang der $z$-Achse nicht beschränkt ist, kann die $z$-Komponente im Verlauf der Bewegung vergleichsweise groß werden, was dann wegen des größeren Abstandes zum Ursprung zur schlechteren Konvergenz von $I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}})$ führt. Für die Abbildungen 4.1 bis 4.3 haben wir als Anfangsbedingungen jeweils $z=0$ und von Bild zu Bild wachsende $p_z$-Werte vorgegeben; deswegen werden die im Lauf der Trajektorien erreichten maximalen $\vert z\vert$-Werte von Bild zu Bild größer und die Quasiintegrale somit divergenter.

Abbildung 4.4, bei der höheren Energie $E=0.20$, zeigt eine andere typische Eigenschaft divergenter formaler Integrale. Hier sieht man den Übergang von anfänglicher Konvergenz ($m=2,\dots,8$) zur Divergenz ($m=8,10,\dots$). Ein Übergang dieser Art ergibt sich für die Brown-Gabrielse-Magnetflasche bei jedem (anfänglich) konvergenten Integral $I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}})$, weil das System nichtintegrabel ist. Der Grad $m_0$, bei dem der Übergang von Konvergenz zur Divergenz stattfindet ($m_0=8$ für das Beispiel in Abbildung 4.4), charakterisiert den Startpunkt ${\mbox{\protect\boldmath$s$}}$ der entsprechenden Trajektorie. Wir werden in Abschnitt 4.3.2 hierauf zurückkommen.

Anhand von Abbildung 4.5 wird deutlich, daß die Divergenz des Quasiintegrals nicht immer langsam eintreten muß, sondern im Gegenteil auch rasant verlaufen kann. Dieses stark divergente, in den vorherigen Abbildungen so nicht zutage tretende Verhalten wird verständlich, wenn man auch hier mit der entsprechenden Poincaré-Abbildung vergleicht: Der Startwert 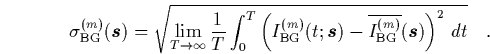${\mbox{\protect\boldmath$s$}}=(0,0.1)^T$ liegt inmitten eines stochastischen Gebietes, das fast die gesamte Poincaré-Fläche ausfüllt; ${\mbox{\protect\boldmath$s$}}$ liegt fern von noch erhalten gebliebenen größeren Inselketten. -- Andererseits gilt, daß auch bei dieser großen Energie immer noch prominente Inseln fast-regulären Verhaltens erhalten geblieben sind. 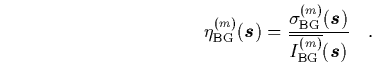Insbesondere ist hier das Inselpaar zu erwähnen, das auf der $p_z$-Achse bei $\vert p_z\vert\approx 0.4$ zu finden ist. Wählt man den Startwert ${\mbox{\protect\boldmath$s$}}$ aus diesem Gebiet, dann ergibt sich lediglich eine relativ moderate Divergenz von $I_{\rm BG}^{(m)}(t;{\mbox{\protect\boldmath$s$}})$, so wie sie in Abbildung 4.6 dargestellt ist.

Schwach divergente oder sogar konvergente Quasiintegrale entsprechen also regulären Gebieten der Poincaré-Fläche, während stärker divergente Quasiintegrale stochastischen Regionen korrespondieren, in denen weniger invariante Tori erhalten geblieben sind.

Mit diesen Beobachtungen haben wir nachgewiesen, daß das berechnete Quasiintegral zumindest für kleine Energien bemerkenswert gut konstant sein kann und dann gute Voraussagen der zeitlichen Entwicklung des Systems erlaubt -- denn (Fast-) Konstanz von $I_{\rm BG}$ heißt ja gerade (Fast-) Integrabilität. Anderenfalls, bei divergentem Quasiintegral, läßt die ,,Geschwindigkeit`` der Divergenz trotzdem noch Schlüsse auf den Grad der Chaotizität des betreffenden Gebietes im Phasenraum zu. Dies ist der Gegenstand des folgenden Abschnitts 4.3.

Eine Analyse des Quasiintegrals nach dem hier beschriebenen Verfahren ist notwendigerweise eine lokale Analyse, denn man nimmt jeweils nur Bezug auf einen einzigen Startwert ${\mbox{\protect\boldmath$s$}}$. In Abschnitt 4.3 wird beschrieben, wie man im Zuge einer globalen Analyse die gesamte Poincaré-Fläche untersuchen kann.