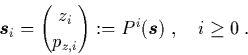 |
(3.23) |
Die in Abschnitt 3.1.2 besprochenen Symmetrieeigenschaften der Brown-Gabrielse-Magnetflasche ermöglichen es, die Iteration der Poincaré-Abbildung und die graphische Darstellung der Resultate sehr effektiv durchzuführen.
Zunächst definieren wir zur Vereinfachung der Notation
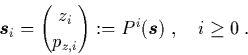 |
(3.23) |
Indem wir die in Abschnitt 3.1.2 diskutierten Symmetrien
ausnutzen, können wir
ohne großen Aufwand erheblich mehr Punkte in den
Poincaré-Plot eintragen als lediglich
die
![]() : Zunächst entnehmen wir aus (3.26c),
daß wir die Bedingung
: Zunächst entnehmen wir aus (3.26c),
daß wir die Bedingung ![]() bei der Erstellung des Poincaré-Plots
gar nicht anwenden müssen. Denn (3.26c) besagt, daß
aus der Existenz des Orbits (3.34) auch die Existenz
eines anderen Orbits in
bei der Erstellung des Poincaré-Plots
gar nicht anwenden müssen. Denn (3.26c) besagt, daß
aus der Existenz des Orbits (3.34) auch die Existenz
eines anderen Orbits in ![]() folgt, der die gleichen Koordinaten
folgt, der die gleichen Koordinaten
![]() und
und ![]() hat, sich aber in
hat, sich aber in ![]() um ein Vorzeichen von
(3.34) unterscheidet. Damit können wir jeden
Durchstoßpunkt der Trajektorie
um ein Vorzeichen von
(3.34) unterscheidet. Damit können wir jeden
Durchstoßpunkt der Trajektorie
![]() durch die
Poincaré-Fläche im Poincaré-Plot markieren.
durch die
Poincaré-Fläche im Poincaré-Plot markieren.
Aus (3.26b) schließen wir, daß auch der am Ursprung
von ![]() punktgespiegelte Orbit ein anderer gültiger Orbit von
punktgespiegelte Orbit ein anderer gültiger Orbit von ![]() ist.
An (3.24b,3.24c) sehen wir
schließlich,
daß wir weitere gültige Orbits in
ist.
An (3.24b,3.24c) sehen wir
schließlich,
daß wir weitere gültige Orbits in ![]() erhalten, indem wir
die Punkte von (3.34) an der
erhalten, indem wir
die Punkte von (3.34) an der ![]() - und der
- und der ![]() -Achse
spiegeln. Denn die Verfolgung des Flusses in negativer Zeitrichtung, die
in (3.24) durch den Parameter
-Achse
spiegeln. Denn die Verfolgung des Flusses in negativer Zeitrichtung, die
in (3.24) durch den Parameter ![]() angedeutet wird,
entspricht der Iteration der Inversen
angedeutet wird,
entspricht der Iteration der Inversen ![]() der Poincaré-Abbildung.
Die Existenz dieser Inversen ist ganz allgemein dadurch sichergestellt,
daß man den Fluß eines Differentialgleichungssystems immer sowohl in
positiver als auch in negativer Zeitrichtung verfolgen kann.
der Poincaré-Abbildung.
Die Existenz dieser Inversen ist ganz allgemein dadurch sichergestellt,
daß man den Fluß eines Differentialgleichungssystems immer sowohl in
positiver als auch in negativer Zeitrichtung verfolgen kann.
Wir haben Poincaré-Schnitte für verschiedene Energien unterhalb der Sattelpunktsenergie 16/27 durchgeführt. Die Ergebnisse dieser numerischen Untersuchungen sind in den Abbildungen 3.7 bis 3.14 dargestellt; dabei haben wir die oben angesprochenen Symmetrien des Systems ausgenutzt. Insgesamt ergibt sich beim Erhöhen des Systemparameters Energie ein typisches KAM-Szenario.
Die Kolmogorov-Arnold-Moser-Theorie -- kurz: KAM-Theorie3.2-- macht Aussagen darüber, welche Tori eines integrablen Hamilton-Systems unter einer kleinen Störung erhalten bleiben, wobei Deformationen der erhaltenen Tori möglich sind. Zunächst stellen wir fest, daß bei einem vierdimensionalen integrablen Hamilton-System die gebundenen Trajektorien auf zweidimensionalen Tori im Phasenraum verlaufen. Im Poincaré-Schnitt zeigen sich diese Tori als invariante Linien -- man vergleiche hierzu die konzentrischen geschlossenen Kurven in Abbildung 3.7 3.3. Die Dynamik auf jedem dieser Tori wird durch zwei Frequenzen charakterisiert. Das System erfüllt die KAM-Bedingung, wenn das Verhältnis der beiden Frequenzen, die Windungszahl, ,,hinreichend irrational`` ist. Wir wollen diese Bedingung hier nicht genauer angeben, weisen aber darauf hin, daß die KAM-Bedingung bei zunehmender Störung im allgemeinen strenger wird. Wenn die KAM-Bedingung und einige weitere ,,technische`` Bedingungen erfüllt sind, dann besagt das KAM-Theorem, daß der entsprechende Torus trotz der Störung des Systems erhalten bleibt.
Im Fall einer rationalen Windungszahl ![]() können wir angeben, was mit
der entsprechenden invarianten Linie geschieht, deren Persistenz ja gerade
nicht durch das KAM-Theorem sichergestellt wird. Hier gilt das Theorem von
Poincaré und Birkhoff: Unter einer Störung bricht der ,,rationale
Torus`` auf und es entstehen
können wir angeben, was mit
der entsprechenden invarianten Linie geschieht, deren Persistenz ja gerade
nicht durch das KAM-Theorem sichergestellt wird. Hier gilt das Theorem von
Poincaré und Birkhoff: Unter einer Störung bricht der ,,rationale
Torus`` auf und es entstehen  elliptische und
elliptische und  hyperbolische
hyperbolische
![]() -periodische Punkte der Poincaré-Abbildung. Dabei ist
-periodische Punkte der Poincaré-Abbildung. Dabei ist ![]() eine
natürliche Zahl; meistens gilt
eine
natürliche Zahl; meistens gilt ![]() [He83]. Die
[He83]. Die ![]() neu entstandenen periodischen Punkte befinden sich dort in
der Poincaré-Fläche, wo vorher die noch nicht aufgebrochene invariante
Linie lag. Zwischen jeweils zwei elliptischen Punkten liegt ein
hyperbolischer Punkt. Eine Poincaré-Birkhoff-Kette -- auch:
,,Inselkette`` -- ist entstanden.
neu entstandenen periodischen Punkte befinden sich dort in
der Poincaré-Fläche, wo vorher die noch nicht aufgebrochene invariante
Linie lag. Zwischen jeweils zwei elliptischen Punkten liegt ein
hyperbolischer Punkt. Eine Poincaré-Birkhoff-Kette -- auch:
,,Inselkette`` -- ist entstanden.
Jeder elliptische periodische Punkt einer Poincaré-Birkhoff-Kette ist seinerseits wieder von invarianten Linien zweiter Ordnung umgeben. Diese Linien unterliegen ebenfalls dem KAM- und dem Poincaré-Birkhoff-Theorem, brechen bei weiter vergrößerter Störung auf und bilden Inselketten zweiter Ordnung. Durch Fortsetzung dieses Szenarios ergibt sich eine sehr komplizierte ineinander geschachtelte Struktur aus invarianten Linien, elliptischen und hyperbolischen periodischen Punkten. Wegen der auf komplexe Weise ineinander verwobenenen stabilen und instabilen Mannigfaltigkeiten3.4der hyperbolischen periodischen Punkte ist die Dynamik in der Umgebung dieser Punkte hochgradig kompliziert und hängt sensibel von den Anfangsbedingungen des betrachteten Orbits ab. Deswegen werden diese Gebiete als ,,stochastische Gebiete`` bezeichnet. Sie sind für die chaotische Komponente der Bewegung verantwortlich und zeigen sich im Poincaré-Plot als Bereiche mit scheinbar regellos verteilten Punkten. Offensichtlich existieren in den stochastischen Gebieten nur noch sehr wenige oder sogar gar keine invarianten Linien. Demnach verläuft die entsprechende Dynamik im Phasenraum typischerweise nicht auf 2-Tori, und das System ist nicht integrabel.
Das oben beschriebene KAM-Szenario läßt sich eindeutig in unseren
Abbildungen 3.7 bis 3.14 wiederfinden.
Trotz größer werdender Störung bleiben
invariante Linien erhalten (man spricht von ,,KAM-Linien``), andererseits
nimmt deren Anzahl mit wachsendem ![]() ab, während die KAM-Bedingung
(vermutlich) strenger wird.
Man erkennt auch die Entstehung von Poincaré-Birkhoff-Ketten erster und
zweiter Ordnung. Die Inselketten dritter und höherer Ordnung sind
in der Regel bereits so
klein, daß man sie in den gezeigten Abbildungen nicht mehr erkennen kann.
Wir haben somit anhand der Poincaré-Plots einen numerischen Nachweis
für die Existenz stochastischer Gebiete und damit für die
Nichtintegrabilität des Systems erbracht.
ab, während die KAM-Bedingung
(vermutlich) strenger wird.
Man erkennt auch die Entstehung von Poincaré-Birkhoff-Ketten erster und
zweiter Ordnung. Die Inselketten dritter und höherer Ordnung sind
in der Regel bereits so
klein, daß man sie in den gezeigten Abbildungen nicht mehr erkennen kann.
Wir haben somit anhand der Poincaré-Plots einen numerischen Nachweis
für die Existenz stochastischer Gebiete und damit für die
Nichtintegrabilität des Systems erbracht.
Es ist an dieser Stelle wichtig festzuhalten, daß wir für das Brown-Gabrielse-System zwar einerseits ein typisches KAM-Szenario finden, andererseits aber weder eine Zerlegung in einen integrablen und einen Störanteil der Hamilton-Funktion angeben, noch die KAM-Bedingung überprüfen können. Unsere Ergebnisse werden also nicht durch das KAM-Theorem erklärt! Es ist aber von Robinson [Ro70], Zehnder [Ze73] und Newhouse [Ne77] gezeigt worden, daß das oben beschriebene KAM-Szenario ganz allgemein eine richtige Beschreibung der Situation in der Nähe eines elliptischen Fixpunktes ist, auch wenn die Bedingungen des KAM-Theorems nicht erfüllt sind. In jedem nichtintegrablen System sind die elliptischen Fixpunkte von invarianten Linien umgeben, auf denen die Bewegung quasiperiodisch, also regulär ist. Darüber hinaus existieren ebenfalls immer Poincaré-Birkhoff-Ketten aus elliptischen und hyperbolischen periodischen Punkten, die die Fixpunkte umschließen. Damit ist auch im nichtintegrablen allgemeinen Fall sichergestellt, daß es stochastische Gebiete und die das KAM-Szenario kennzeichnende Koexistenz von regulärer und chaotischer Dynamik gibt.
Wir bemerken an dieser Stelle noch, daß der Ursprung
![]() der Poincaré-Fläche für alle
der Poincaré-Fläche für alle ![]() ein Fixpunkt der Poincaré-Abbildung
ist. Denn startet man einen Orbit mit der Anfangsbedingung
ein Fixpunkt der Poincaré-Abbildung
ist. Denn startet man einen Orbit mit der Anfangsbedingung
![]() , dann erhält man aus Gl. (3.6)
, dann erhält man aus Gl. (3.6) 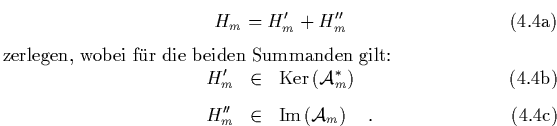 für alle Zeiten.
Der Orbit verläßt demnach die
für alle Zeiten.
Der Orbit verläßt demnach die ![]() -Achse nie, so daß für alle seine
Schnittpunkte mit der
-Achse nie, so daß für alle seine
Schnittpunkte mit der ![]() -Achse
-Achse
![]() gilt.
Besondere Beachtung verdient
die Entwicklung des Stabilitätstypus dieses Fixpunktes:
Bei niedrigen Energien handelt es sich natürlich um einen elliptischen
Fixpunkt. Bei einer knapp unterhalb von
gilt.
Besondere Beachtung verdient
die Entwicklung des Stabilitätstypus dieses Fixpunktes:
Bei niedrigen Energien handelt es sich natürlich um einen elliptischen
Fixpunkt. Bei einer knapp unterhalb von 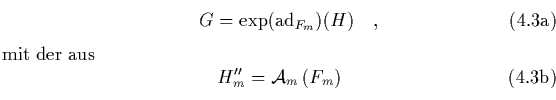 liegenden Energie
verwandelt er sich in einen instabilen Fixpunkt, um dann bei einem
Energiewert zwischen
liegenden Energie
verwandelt er sich in einen instabilen Fixpunkt, um dann bei einem
Energiewert zwischen ![]() und
und ![]() wieder stabil zu werden.
Man vergleiche hierzu die Abbildungen 3.11, 3.12
und 3.13.
wieder stabil zu werden.
Man vergleiche hierzu die Abbildungen 3.11, 3.12
und 3.13.
Nachdem wir uns in diesem Kapitel einen qualitativen Überblick über die Dynamik in der Brown-Gabrielse-Magnetflasche verschafft haben, gilt es nun, den in Kapitel 1 entwickelten Formalismus der Normalformentheorie anzuwenden. Wir werden im folgenden Kapitel sehen, daß es in der Tat möglich ist, mit seiner Hilfe weitergehende Informationen über unser System zu erhalten.