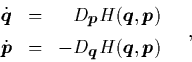Theorie der Normalformen und Quasiintegrale

Everything should be made as simple as possible,

but not simpler.

ALBERT EINSTEIN

In diesem Kapitel diskutieren wir Verfahren, mittels derer ein Hamiltonsches dynamisches System,

$$\quad \begin{array}{ccr} \dot{{\mbox{\protect\boldmath$q$... ...ldmath$q$}},{\mbox{\protect\boldmath$p$}}) \end{array} \quad,$$ (1.1)

also ein System von $2n$ gekoppelten Differentialgleichungen erster Ordnung, das sich aus einer Hamilton-Funktion $H({\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}})$ herleiten läßt, gezielt vereinfacht werden kann. Wir betrachten an dieser Stelle noch kein spezielles physikalisches System, sondern halten die Diskussion so allgemein wie möglich. Dementsprechend sind hier die ${\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}} \in {\bf R}^n$ ein beliebiger vollständiger Satz von zueinander kanonisch-konjugierten Koordinaten bzw. Impulsen.

Wir beschränken uns der Einfachheit halber auf autonome Systeme. Die hier dargestellten Verfahren lassen sich aber prinzipiell auch auf zeitabhängige Systeme übertragen. Man vergleiche hierzu beispielsweise [Ar83,Oz88].

Die jeglicher ,,Normalformentheorie`` zugrunde liegende Idee ist es, das betrachtete System so weit wie möglich zu vereinfachen, ohne dabei charakteristische Systemeigenschaften zu verlieren. Man möchte eine ganze Klasse von Objekten auf einen einzigen typischen und möglichst einfachen Vertreter dieser Klasse zurückführen. Dabei ist entscheidend, daß man aus den Eigenschaften der Normalform diejenigen des zu untersuchenden Systems folgern können muß [NaSc61]. Man fordert also die -- in jedem einzelnen Fall noch genauer zu spezifizierende -- Äquivalenz des Ausgangssystems und seiner Normalform.

Was nun ,,Vereinfachung`` konkret bedeutet, hängt von der Art des zu untersuchenden Systems ab. Es gibt entsprechende Theorien für gewöhnliche und partielle Differentialgleichungen, diskrete Abbildungen, Matrizen usw. In der linearen Algebra wird beispielsweise die Jordansche Normalform einer quadratischen Matrix diskutiert (siehe zum Beispiel [Fi86]): Jede komplexe $(n,n)$-Matrix $A$ kann durch eine Ähnlichkeitstransformation (die in diesem Fall die angesprochene Äquivalenz sicherstellt) mit einer unitären $(n,n)$-Matrix $X$ auf Jordansche Normalform $J$ gebracht werden,

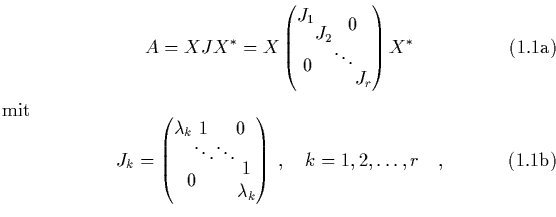
wobei die Dimension des Jordan-Blockes $J_k$ der algebraischen Vielfachheit des Eigenwertes $\lambda_k$ als Nullstelle des charakteristischen Polynoms von $A$ entspricht. $J$ stellt eine erhebliche Vereinfachung gegenüber $A$ dar und geht eindeutig und umkehrbar aus $A$ hervor. Normalformentheorie für Differentialgleichungen oder Hamilton-Funktionen ist aber im allgemeinen erheblich komplizierter als Normalformentheorie für Matrizen, weil die benötigten Transformationen, anders als $X$ in Gl. (1.2a), nichtlinear sind.

Der historischen Entwicklung folgend und um das weitere Vorgehen zu motivieren, gehen wir zunächst auf die von Poincaré [Po92] begründete Normalformentheorie beliebiger, nicht notwendigerweise Hamiltonscher Differentialgleichungen ein. Wir stützen uns dabei vor allem auf die modernere Diskussion in [Ar83].

Es zeigt sich bald, daß es vorteilhaft ist, nicht das Vektorfeld der Differentialgleichung, sondern die entsprechende Hamilton-Funktion zu untersuchen, falls das vorliegende System ein Hamilton-System ist. Deshalb diskutieren wir im Anschluß an die allgemeine Theorie die spezielle Normalformentheorie für Hamilton-Systeme. Die klassische Theorie geht auf Birkhoff [Bi66] zurück. Eine modernere und allgemeinere Darstellung der Birkhoffschen Theorie gab Gustavson [Gu66]; in dieser Form wird die Normalformentheorie für Hamilton-Funktionen bis heute vielfach angewendet (vgl. [SaVe85,Oz88,KaRo92]). Allerdings kann auch die Gustavsonsche Theorie nicht auf sämtliche Hamilton-Funktionen angewendet werden.

Dragt und Finn [DrFi76a,DrFi79] formulierten den Gustavsonschen Formalismus in der Sprache der Lie-Transformationstheorie [Ga68,De69,Ca81,LiLi92], welche eine erheblich übersichtlichere Darstellung der Transformation auf Normalform ermöglicht. Im Gegensatz zu Gustavsons Methode, bei der die Erzeugende der Transformation sowohl von den alten als auch den neuen Koordinaten abhängt, treten bei Dragt und Finn solche ,,gemischten`` Variablensätze nicht auf. Darüber hinaus gelingt mit Hilfe von Lie-Transformationen die Erweiterung der Hamiltonschen Normalformentheorie auf beliebige Hamilton-Funktionen, die in Form einer formalen Potenzreihe vorliegen. Die ersten Schritte in diese Richtung wurden ebenfalls von Dragt und Finn in [DrFi79] unternommen und von Stegemerten [St91] und Meyer und Hall [MeHa92] zu einer umfassenden Theorie ausgebaut.

Eines der zentralen Anliegen der Theorie dynamischer Systeme ist die Bestimmung von Integralen der Bewegung, soweit diese überhaupt existieren. Ein Integral der Bewegung (oder auch: Konstante der Bewegung) ist eine Funktion $I({\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}})$, die entlang jeder Flußlinie (Trajektorie) des Differentialgleichungssystems (1.1) konstant ist. Die Existenz eines solchen Integrals der Bewegung bedeutet eine erhebliche Vereinfachung der Dynamik, weil dadurch jede Trajektorie auf eine der durch $I({\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}})=\mbox{konst.}$ definierten Hyperflächen im Phasenraum beschränkt ist. Somit wird die Dimension des betrachteten Problems um eins reduziert. Dementsprechend ist die Kenntnis eines weiteren Integrals (zusätzlich zu den ohnehin schon bekannten Integralen) gleichbedeutend mit einer wesentlichen zusätzlichen Information über das System. Die Existenz mehrerer voneinander unabhängiger Integrale der Bewegung^1.1 $I_j({\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}})$ zieht eine weitere Vereinfachung nach sich, denn die Trajektorien können in diesem Fall den Durchschnitt der durch die Invarianz der $I_j$ gegebenen Hyperflächen nicht verlassen. Wenn es sogar $n$ voneinander unabhängige Integrale der Bewegung gibt, also ebensoviele wie Freiheitsgrade der Bewegung, dann gilt im Fall gebundener Bewegung das Liouville-Arnold-Theorem [Ar89]. Es besagt, daß die Trajektorien (quasi-) periodisch auf einem $n$-Torus verlaufen, so daß die Dynamik des Systems vollständig geordnet und nicht chaotisch ist.

Die Suche nach weiteren Integralen der Bewegung ist demnach ein wichtiges Verfahren zur Analyse dynamischer Systeme. Speziell im Fall zweier Freiheitsgrade der Bewegung ($n=2$) bedeutet die Existenz eines zweiten Integrals der Bewegung -- neben $H({\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}})$ -- die vollständige Integrabilität des Systems. In [Hi87] findet man eine umfassende Darstellung der bekannten Methoden für die Suche nach diesem zweiten Integral für $n=2$. Es bleibt aber festzustellen, daß es kein allgemeines Verfahren für diese Suche gibt. Ohnehin sind die meisten Hamilton-Systeme nicht integrabel.

Wie hängen nun die Normalformentheorie und die Suche nach Integralen der Bewegung zusammen? Im Hénon-Heiles-System, einem zweidimensionalen autonomen Hamilton-System, findet man [HeHe64] unter gewissen Bedingungen empirisch, das heißt durch die numerische Integration der kanonischen Gleichungen und Analyse des so entstehenden Phasenportraits, die Existenz eines zweiten Integrals der Bewegung. Für eine Vielzahl von weiteren Modellsystemen gibt es gleichlautende Befunde. Unter anderem um diese Ergebnisse zu erklären, entwarf Gustavson seine Normalformentheorie. Deren Anwendung ermöglicht die konsistente Konstruktion von Näherungsformeln für die experimentell gefundenen Integrale. Eine wesentliche Anwendung auch der Dragt-Finn-Stegemertenschen Normalform eines Hamilton-Systemes ist die systematische Konstruktion eines formalen Integrals der Bewegung, das -- neben der Hamilton-Funktion -- eine zweite Konstante der Bewegung darstellt, falls die Normalformtransformation konvergiert. Damit erweist sich die zunächst als l'art pour l'art anmutende Normalformentheorie als mächtiges Werkzeug in der Theorie dynamischer Systeme.

Man spricht allerdings in diesem Zusammenhang von Quasiintegralen anstelle von Integralen der Bewegung, weil man mit Hilfe der Normalformentheorie im allgemeinen nur Näherungsformeln für die gesuchten Integrale bestimmen kann.

Fußnoten

... Bewegung^1.1

Zur Definition der ,,Unabhängigkeit`` von Integralen der Bewegung vergleiche Abschnitt 1.2.4.