Wir kommen nun zur grundlegenden Idee der Normalformentheorie für
Hamilton-Systeme. Das Ziel ist es, die Hamilton-Funktion dahingehend
zu vereinfachen, daß man ein zweites Integral der Bewegung angeben
kann.1.7Insbesondere für Systeme mit zwei Freiheitsgraden der Bewegung (![]() )
ist klar, daß das Auffinden eines zweiten Integrals eine wesentliche
Vereinfachung darstellt, denn damit wäre das Problem bereits vollständig
gelöst: Das System besäße die größtmögliche Anzahl voneinander
unabhängiger Integrale und das Liouville-Arnold-Theorem wäre anwendbar,
falls die Bewegung gebunden ist. Zudem könnten wir
den 2-Torus, auf dem alle Trajektorien verlaufen, durch die beiden
bekannten Integrale vollständig charakterisieren und hätten somit ein
vollständige geometrische Beschreibung des Phasenflusses.
Im Rahmen der Gustavsonschen Normalformentheorie [Gu66]
versucht man, die Hamilton-Funktion so zu transformieren, daß der
quadratische Anteil
)
ist klar, daß das Auffinden eines zweiten Integrals eine wesentliche
Vereinfachung darstellt, denn damit wäre das Problem bereits vollständig
gelöst: Das System besäße die größtmögliche Anzahl voneinander
unabhängiger Integrale und das Liouville-Arnold-Theorem wäre anwendbar,
falls die Bewegung gebunden ist. Zudem könnten wir
den 2-Torus, auf dem alle Trajektorien verlaufen, durch die beiden
bekannten Integrale vollständig charakterisieren und hätten somit ein
vollständige geometrische Beschreibung des Phasenflusses.
Im Rahmen der Gustavsonschen Normalformentheorie [Gu66]
versucht man, die Hamilton-Funktion so zu transformieren, daß der
quadratische Anteil
![]() der transformierten Hamilton-Funktion
zu einem Integral der Bewegung wird.
der transformierten Hamilton-Funktion
zu einem Integral der Bewegung wird.
Wir stellen Gustavsons Verfahren hier nicht in seiner ursprünglichen Formulierung dar, sondern bedienen uns der Lie-Transformationstheorie. Stegemerten [St91] demonstriert, daß man auf diese Weise die gleichen Ergebnisse erhält wie bei Verwendung von Gustavsons Formulierung. Der entscheidende Vorteil unserer Vorgehensweise liegt darin, daß alle auftretenden Ausdrücke erheblich einfacher und übersichtlicher notiert werden können. Zudem werden wir so auf natürliche Weise zu der in Abschnitt 1.2.3 dargestellten Verallgemeinerung geführt.
Man sagt, daß
![]() in Gustavson-Normalform bis zum Grad
in Gustavson-Normalform bis zum Grad ![]() ist, wenn gilt:
ist, wenn gilt:
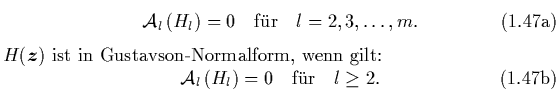
Im Rahmen der Gustavsonschen Theorie werden also nur solche Systeme
behandelt, die in niedrigster Ordnung (1.61) durch ![]() harmonische Oszillatoren mit den Frequenzen
harmonische Oszillatoren mit den Frequenzen ![]() beschrieben werden können.
Die Anteile der Hamilton-Funktion mit größerem Grad
als 2,
beschrieben werden können.
Die Anteile der Hamilton-Funktion mit größerem Grad
als 2,
![]() , beschreiben die
Anharmonizitäten und anharmonischen
Kopplungen dieser Oszillatoren, die im allgemeinen zu einer beliebig
komplizierten Dynamik führen. Der Grund für die einschränkende
Forderung nach diesem
, beschreiben die
Anharmonizitäten und anharmonischen
Kopplungen dieser Oszillatoren, die im allgemeinen zu einer beliebig
komplizierten Dynamik führen. Der Grund für die einschränkende
Forderung nach diesem ![]() -Typ wird im folgenden Abschnitt
1.2.3 diskutiert.
-Typ wird im folgenden Abschnitt
1.2.3 diskutiert.
Es liegt auf der Hand, daß diese Normalformdefinition im Hinblick auf die
gewünschte Vereinfachung des Systems sinnvoll ist, denn offensichtlich
ist der quadratische Anteil der Hamilton-Funktion ein Integral der
Bewegung, wenn
![]() in Gustavson-Normalform ist:
in Gustavson-Normalform ist:
 |
(1.47) |
Wenn eine beliebige Hamilton-Funktion vom Typ
(1.61) gegeben ist, dann ist
![]() selbstverständlich noch kein Integral der Bewegung. Vielmehr müssen wir
selbstverständlich noch kein Integral der Bewegung. Vielmehr müssen wir
![]() zunächst auf Normalform transformieren und erst nach
dieser Transformation, in den entsprechenden neuen Koordinaten
zunächst auf Normalform transformieren und erst nach
dieser Transformation, in den entsprechenden neuen Koordinaten
![]() , ist
, ist
![]() konstant.
Transformiert man dann diese Konstante der Bewegung zurück auf die
ursprünglichen Koordinaten
konstant.
Transformiert man dann diese Konstante der Bewegung zurück auf die
ursprünglichen Koordinaten ![]() , so erhält man das zweite Integral der
Bewegung als eine Funktion von
, so erhält man das zweite Integral der
Bewegung als eine Funktion von
![]() , die im allgemeinen nicht nur aus
quadratischen Termen besteht.
, die im allgemeinen nicht nur aus
quadratischen Termen besteht.
Um eine gegebene Hamilton-Funktion ![]() in eine neue Hamilton-Funktion
in eine neue Hamilton-Funktion
![]() zu transformieren, die in Gustavson-Normalform ist,
bedienen wir uns einer (unendlichen) Folge von Lie-Transformationen
zu transformieren, die in Gustavson-Normalform ist,
bedienen wir uns einer (unendlichen) Folge von Lie-Transformationen
![]() ,
die jeweils einem
Grad
,
die jeweils einem
Grad ![]() -Polynom mit
-Polynom mit ![]() assoziiert sind:
assoziiert sind:
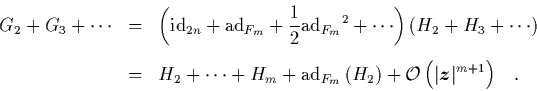
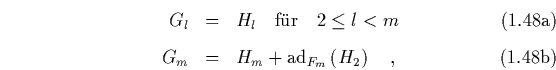
Die Hamilton-Funktion ![]() sei bis zum Grad
sei bis zum Grad ![]() in
Gustavson-Normalform. Die Transformation (1.64) ergibt wegen
Gl. (1.65a) eine neue Hamilton-Funktion
in
Gustavson-Normalform. Die Transformation (1.64) ergibt wegen
Gl. (1.65a) eine neue Hamilton-Funktion
![]() , die ebenfalls in Normalform bis
mindestens zum Grad
, die ebenfalls in Normalform bis
mindestens zum Grad ![]() ist. Unter Berücksichtigung von Gl. (1.65b) können wir durch eine geeignete Wahl von
ist. Unter Berücksichtigung von Gl. (1.65b) können wir durch eine geeignete Wahl von ![]() außerdem erreichen, daß
außerdem erreichen, daß ![]() sogar in Normalform bis zum Grad
sogar in Normalform bis zum Grad ![]() ist.
Mit
ist.
Mit
![]() erhalten
wir aus Gl. (1.65b) die Gleichung
erhalten
wir aus Gl. (1.65b) die Gleichung
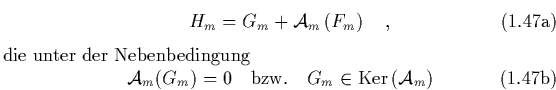
zu lösen ist. Analog zur Situation in Abschnitt 1.1
sind ![]() und
und ![]() gegeben;
gegeben; ![]() und
und ![]() sind gesucht.
sind gesucht.
![]() ist der Kern des Operators
ist der Kern des Operators ![]() :
:
| (1.47) |
Ebenso wie in der Normalformentheorie für Vektorfelder haben wir also
eine homologische Gleichung (1.66a)
zu lösen. Aus den bekannten ![]() und
und ![]() sind die Grad
sind die Grad ![]() -Polynome
-Polynome
![]() und
und ![]() zu bestimmen. Die Lösung gelingt mit Hilfe der Zerlegung
von
zu bestimmen. Die Lösung gelingt mit Hilfe der Zerlegung
von ![]() in die direkte Summe des Kernes und des Bildes von
in die direkte Summe des Kernes und des Bildes von ![]() :
:
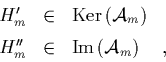 |
(1.50) |

Wir weisen jetzt die Gültigkeit der Zerlegung
(1.68) nach
und zeigen im Verlauf des Beweises auch, wie ein Urbild
von ![]() unter
unter ![]() gefunden werden kann.
Für
gefunden werden kann.
Für ![]() gilt
gilt
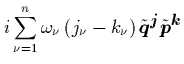 |
|||
| (1.53) |
Die letzte Gleichung ist eine Eigenwertgleichung mit dem Eigenvektor
![]() zum Eigenwert
zum Eigenwert
![]() .
Demnach können wir den Kern und das Bild von
.
Demnach können wir den Kern und das Bild von
![]() angeben
als die lineare Hülle derjenigen
angeben
als die lineare Hülle derjenigen
![]() , für die der
Eigenwert null bzw. von null verschieden ist:
, für die der
Eigenwert null bzw. von null verschieden ist:
| (1.55) |
Gl. (1.76) zeigt auch, wie man die Zerlegung von ![]() gemäß Gl. (1.69) findet und wie das für Gl. (1.71b) benötigte Urbild von
gemäß Gl. (1.69) findet und wie das für Gl. (1.71b) benötigte Urbild von ![]() bestimmt werden
kann. Dazu
muß zunächst
bestimmt werden
kann. Dazu
muß zunächst ![]() auf die Variablen
auf die Variablen
![]() transformiert werden:
transformiert werden:
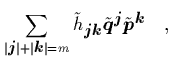 |
(1.56) |
Insgesamt haben wir den folgenden Satz bewiesen:
Dieser Satz wurde schon von Gustavson in [Gu66] angegeben.
Allerdings ist Gustavsons Darstellung erheblich schwerfälliger, weil
sie nicht auf der Theorie der Lie-Transformationen beruht, sondern für
die kanonischen Transformationen erzeugende Funktionen vom ![]() -Typ
(vgl. [Go80]) verwendet.
In der Formulierung, die in der vorliegenden Arbeit benutzt wird, findet
sich Satz 1.2 beispielsweise auch in [St91].
-Typ
(vgl. [Go80]) verwendet.
In der Formulierung, die in der vorliegenden Arbeit benutzt wird, findet
sich Satz 1.2 beispielsweise auch in [St91].