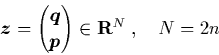Resonanz bei Hamiltonschen Vektorfeldern

Wir zeigen in diesem Abschnitt, daß das Auftreten von Resonanztermen bei Hamiltonschen Vektorfeldern nicht ausgeschlossen werden kann, so daß es im allgemeinen nicht möglich ist, mit der dargestellten Normalisierungsprozedur die Hamiltonschen Differentialgleichungen vollständig zu lösen.

Wir bringen zunächst die kanonischen Gleichungen (1.1) auf die Gestalt der Gl. (1.3), indem wir

$${\mbox{\protect\boldmath$z$}} = {{\mbox{\protect\boldmath$q... ...{\mbox{\protect\boldmath$p$}}} \in {\bf R}^{N} \;, \quad N=2n$$ (1.20)

setzen und damit zu

$$\dot{{\mbox{\protect\boldmath$z$}}} = \left( \begin{array}{@{}r@{}} D_{\mbox{\protect\footnotesize\prot... ...\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}}) \end{array} \right)$$

$$= J D_{\mbox{\protect\footnotesize\protect\boldmath$z$}}H({\mbox{\protect\boldmath$z$}})$$ (1.21)

übergehen. $J$ bezeichnet hier die symplektische Matrix

$$\quad J = \left( \begin{array}{cc} 0 & \mbox{\rm id}_n \\ -\mbox{\rm id}_n & 0 \end{array} \right) \quad.$$ (1.22)

Wenn wir uns, analog zur Diskussion für allgemeine Vektorfelder, auf Hamilton-Funktionen beschränken, die als Potenzreihe vorliegen und in ${\bf0}$ einen kritischen Punkt haben, ergibt die Linearisierung von (1.31) um ${\bf0}$:

$$\dot{{\mbox{\protect\boldmath$z$}}} = J D_{\mbox{\protect\footnotesize\protect\boldmath$z$}}H_2({\mbox{... ...math$z$}}) + {{\cal O}\left(\vert{\mbox{\protect\boldmath$z$}}\vert^{2}\right)}$$

$$= L{\mbox{\protect\boldmath$z$}} + {{\cal O}\left(\vert{\mbox{\protect\boldmath$z$}}\vert^{2}\right)}$$ (1.23)

mit der Hamilton-Matrix [Oz88]

$$\quad L = J\; \mbox{Hess}(H_2({\mbox{\protect\boldmath$z$}})) \quad,$$ (1.24)

wobei $H_2({\mbox{\protect\boldmath$z$}})$ für den quadratischen Anteil von $H({\mbox{\protect\boldmath$z$}})$ steht und $\mbox{Hess}(H_2)$ die Hesse-Matrix von $H_2({\mbox{\protect\boldmath$z$}})$ bezeichnet:

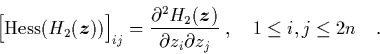$$\quad \Big[ \mbox{Hess}(H_2({\mbox{\protect\boldmath$z$}})... ...}{\partial z_i \partial z_j} \;,\quad 1\leq i,j\leq 2n \quad.$$ (1.25)

In [St87] wird gezeigt, daß die Flußabbildung $M(t)=\exp(Lt)$ des linearisierten Hamilton-Systems symplektisch ist:

$$\quad M^T J M = J \quad.$$ (1.26)

Wegen der Symplektizität ist mit $\mu$ auch $$\frac{1}{\mu}$$ Eigenwert von $M(t)$, denn

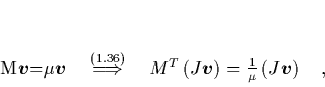$$% latex2html id marker 1056\quad M{\mbox{\protect\boldma... ...frac{1}{\mu}\left(J{\mbox{\protect\boldmath$v$}}\right) \quad,$$ (1.27)

und $M$ und $M^T$ haben dieselben Eigenwerte. Dies hat schließlich zur Folge, daß die Eigenwerte von $L$ nur als Paare $\lambda,-\lambda$ auftreten.

Um nachzuweisen, daß Anteile des Hamiltonschen Vektorfeldes resonant sein können, müssen wir die Nichtinvertierbarkeit von ${\cal B}_l$ zeigen: $\mbox{Im}\left({\cal B}_l\right)\neq\H_l$. Wir führen diesen Nachweis hier nur für den Fall, daß $L$ diagonalisierbar ist: Der Fall nichttrivialer Jordanblöcke von $L$ wird in [Ar83,ArPl90] diskutiert und führt zum gleichen Ergebnis.

$\{{\mbox{\protect\boldmath$e$}}_j\vert j=1,2,\ldots,2n\}$ sei eine Basis, in der $L$ diagonal ist:

$$\quad L{\mbox{\protect\boldmath$e$}}_j = \lambda_j{\mbox{\protect\boldmath$e$}}_j \quad.$$ (1.28)

Wir berechnen die Bilder der Basisvektoren $\left\{ {\mbox{\protect\boldmath$z$}}^{\mbox{\protect\footnotesize\protect\bold... ...j \Big\vert \vert{\mbox{\protect\boldmath$m$}}\vert=l, j=1,2,\ldots,2n \right\}$ von $\H_l$ unter ${\cal B}_l$:

$$\quad {\cal B}_l\left({\mbox{\protect\boldmath$z$}}^{\mbox{\protect\footnotesize\protect\boldmath$m$}}{\mbox{\protect\boldmath$e$}}_j\right) = D\left({\mbox{\protect\boldmath$z$}}^{\mbox{\protect\footnotesize... ...mbox{\protect\footnotesize\protect\boldmath$m$}}{\mbox{\protect\boldmath$e$}}_j$$

$$= \left( {\mbox{\protect\boldmath$m$}}\mbox{\protect\boldmath$\cdot... ...ootnotesize\protect\boldmath$m$}}{\mbox{\protect\boldmath$e$}}_j \right) \quad,$$ (1.29)

wobei wir noch ${\mbox{\protect\boldmath$\lambda$}}:=(\lambda_1,\lambda_2,\ldots,\lambda_{2n})^T$ gesetzt und das gewöhnliche Skalarprodukt im ${\bf R}^{2n}$, ${\mbox{\protect\boldmath$a$}}\mbox{\protect\boldmath$\cdot$}{\mbox{\protect\boldmath$b$}}=\sum_{i=1}^{2n} a_ib_i$, verwendet haben. $\left( {\mbox{\protect\boldmath$m$}}\mbox{\protect\boldmath$\cdot$}{\mbox{\protect\boldmath$\lambda$}}-\lambda_j \right)$ ist also ein Eigenwert von ${\cal B}_l$ zum Eigenvektor ${\mbox{\protect\boldmath$z$}}^{\mbox{\protect\footnotesize\protect\boldmath$m$}}{\mbox{\protect\boldmath$e$}}_j$. Genau dann, wenn die Eigenwerte $\lambda_i$ von $L$ die Resonanzbedingung

$$\lambda_j = {\mbox{\protect\boldmath$m$}}\mbox{\protect\boldmath$\cdot$}{\mbox{\protect\boldmath$\lambda$}}$$ (1.30)

für ein ${\mbox{\protect\boldmath$m$}}$ mit $\vert{\mbox{\protect\boldmath$m$}}\vert=l\geq 2$ und für ein $1\leq j\leq 2n$ erfüllen, wenn ${\cal B}_l$ also den Eigenwert 0 hat, gilt ${\cal N}_l\neq\emptyset$, und die homologische Gleichung kann nicht mehr in jedem Fall gelöst werden, weil ${\cal B}_l$ nicht invertierbar ist.

Die Resonanzbedingung ist für Hamilton-Systeme immer erfüllt: $\lambda_1=\lambda$ und $\lambda_2=-\lambda$ seien eines der Eigenwertpaare, deren Existenz wir oben nachgewiesen haben. Mit ${\mbox{\protect\boldmath$m$}}=(2,1,0,\ldots,0)^T$ und $j=1$ ist dann Gl. (1.40) erfüllt.

Damit ist klar, daß die Normalformentheorie allgemeiner Vektorfelder, angewandt auf Hamiltonsche Vektorfelder, kein geeignetes Werkzeug zur Vereinfachung darstellt, denn die Linearisierbarkeit ist auf diesem Wege keineswegs sichergestellt. Zwar führt auch die Normalformentheorie für Hamilton-Funktionen nicht auf eine Linearisierung, aber die geforderte Vereinfachung gelingt hier auf andere Weise, wie wir in Abschnitt 1.2 sehen werden.