Weil ![]() nur quadratisch von
nur quadratisch von ![]() und
und ![]() abhängt, ist
abhängt, ist
![]() symmetrisch bezüglich der
symmetrisch bezüglich der ![]() - und der
- und der ![]() -Achse:
-Achse:
| (3.12) |
Aus der Hamilton-Funktion
 ergeben sich die folgenden kanonischen Gleichungen:
ergeben sich die folgenden kanonischen Gleichungen:
| (3.13) |
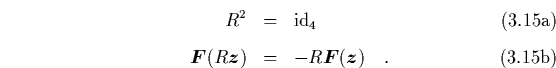 gesetzt mit
gesetzt mit
Nach [Mo73] nennt man ein vierdimensionales dynamisches System
![]() reversibel, wenn es eine lineare Abbildung
reversibel, wenn es eine lineare Abbildung
![]() gibt, für die gilt:
gibt, für die gilt:
![]()
Die Abbildung ![]() wird als Reflexion bezeichnet. Die Bedeutung
der Eigenschaft (3.20b) liegt darin, daß mit
wird als Reflexion bezeichnet. Die Bedeutung
der Eigenschaft (3.20b) liegt darin, daß mit
![]() auch
auch
![]() eine Lösung von Gl. (3.18) ist, denn es gilt:
eine Lösung von Gl. (3.18) ist, denn es gilt:
Wir beschränken uns hier auf Reflexionen der Form
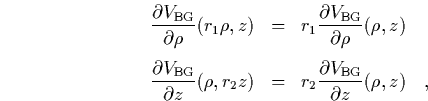 . Gl. (3.20a) zieht dann
. Gl. (3.20a) zieht dann 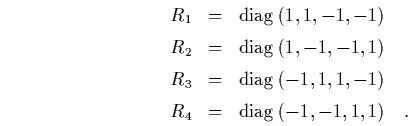 ,
,
| (3.16) |
Wir haben damit gefunden, daß mit der Lösung
![]()
Lösungen der kanonischen Gleichungen sind.
Durch Kombination zweier Reflexionen kann man weitere Lösungen der
kanonischen Gleichungen erhalten. Es sei
![]() eine Lösung von
Gl. (3.18). Wir konstruieren daraus mit Hilfe von Gl. (3.21) die neue Lösung
eine Lösung von
Gl. (3.18). Wir konstruieren daraus mit Hilfe von Gl. (3.21) die neue Lösung
![]() , wobei
, wobei
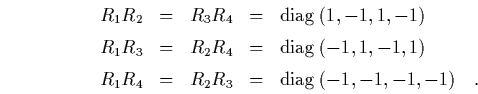 eine der Reflexionen aus Gl. (3.23)
ist. Die nochmalige Anwendung der
Reversibilitätsbedingung (3.20b) mit
eine der Reflexionen aus Gl. (3.23)
ist. Die nochmalige Anwendung der
Reversibilitätsbedingung (3.20b) mit 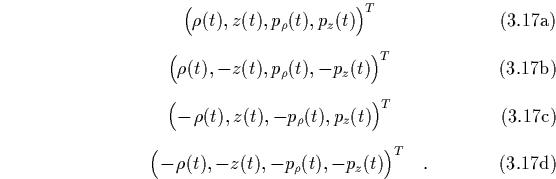 ergibt dann die
weitere Lösung
ergibt dann die
weitere Lösung
![]() .
Eine neue Lösung dieses Typs zeichnet sich gegenüber der in Gl. (3.21) beschriebenen Lösung
.
Eine neue Lösung dieses Typs zeichnet sich gegenüber der in Gl. (3.21) beschriebenen Lösung
![]() dadurch
aus,
daß wir hier keine Zeitumkehr vorzunehmen haben.
dadurch
aus,
daß wir hier keine Zeitumkehr vorzunehmen haben.
![]() beschreibt also eine Trajektorie, die man durch
Anwendung der Flußabbildung
beschreibt also eine Trajektorie, die man durch
Anwendung der Flußabbildung ![]() in positiver Zeitrichtung
erhält.
in positiver Zeitrichtung
erhält.
Es gibt sechs Möglichkeiten, jeweils zwei ![]() miteinander zu
kombinieren:
miteinander zu
kombinieren:
| (3.17) |
Für die praktische Analyse des Systems sind die hier angesprochenen Symmetrieeigenschaften sehr nützlich. Sie ermöglichen es, den numerischen Aufwand für die Berechnung der im nachfolgenden Abschnitt zu besprechenden Poincaré-Schnitte erheblich zu reduzieren.