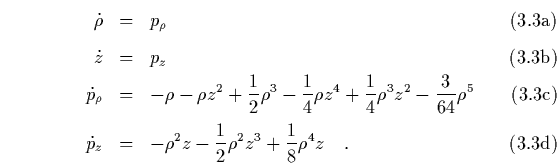 bis ins Unendliche. Deshalb ist der gebundene Charakter
der Teilchenbahnen nicht offensichtlich.
bis ins Unendliche. Deshalb ist der gebundene Charakter
der Teilchenbahnen nicht offensichtlich.
In diesem Abschnitt gehen wir der Frage nach,
ob in dem Brown-Gabrielse-Potential
![]() gebundene Bewegungen möglich sind.
Zur Beantwortung dieser Frage sucht man gewöhnlich isolierte lokale
Minima des
Potentials, weil diese Ljapunov-stabil sind und somit in einer
hinreichend kleinen Umgebung
eine gebundene Bewegung ermöglichen [Ar89].
Dieses Verfahren ist aber im Falle von
gebundene Bewegungen möglich sind.
Zur Beantwortung dieser Frage sucht man gewöhnlich isolierte lokale
Minima des
Potentials, weil diese Ljapunov-stabil sind und somit in einer
hinreichend kleinen Umgebung
eine gebundene Bewegung ermöglichen [Ar89].
Dieses Verfahren ist aber im Falle von ![]() nicht anwendbar,
weil es keine isolierten Minima gibt.
Vielmehr
sind die Punkte minimalen Potentials hier die durch die Gln. (3.5a,3.5b) beschriebenen
Kurven
nicht anwendbar,
weil es keine isolierten Minima gibt.
Vielmehr
sind die Punkte minimalen Potentials hier die durch die Gln. (3.5a,3.5b) beschriebenen
Kurven
![]() in der
in der ![]() -Ebene.
Darüber hinaus ist der zugängliche Teil des Konfigurationsraumes sogar für
Teilchen mit niedriger Energie
-Ebene.
Darüber hinaus ist der zugängliche Teil des Konfigurationsraumes sogar für
Teilchen mit niedriger Energie ![]() nicht beschränkt, wie die Abbildung
3.2 zeigt: Das Gebiet mit
nicht beschränkt, wie die Abbildung
3.2 zeigt: Das Gebiet mit
![]() erstreckt sich in der Nähe der
erstreckt sich in der Nähe der ![]() -Achse und ebenso entlang der Linien
-Achse und ebenso entlang der Linien
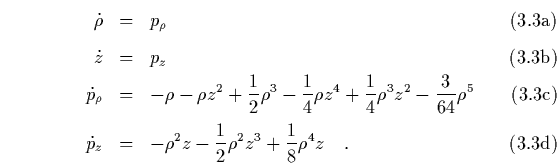 bis ins Unendliche. Deshalb ist der gebundene Charakter
der Teilchenbahnen nicht offensichtlich.
bis ins Unendliche. Deshalb ist der gebundene Charakter
der Teilchenbahnen nicht offensichtlich.
Andererseits veranschaulicht aber die Abbildung 3.2,
daß fast alle Trajektorien -- alle bis auf diejenigen, die auf der
![]() -Achse mit verschwindendem Radialimpuls
-Achse mit verschwindendem Radialimpuls ![]() starten -- irgendwann
auf eine der ,,Potentialwände`` stoßen, die die Potentialmulden um
starten -- irgendwann
auf eine der ,,Potentialwände`` stoßen, die die Potentialmulden um
![]() herum einschließen. Die Trajektorien werden dort
reflektiert,
was schließlich nach einigen solcher Reflexionen
dazu führt,
daß die ursprünglich auslaufende Trajektorie wieder in die Nähe
des Ursprungs zurückkehrt.
In Abbildung 3.3 zeigen wir diesen Einschlußmechanismus
an einem typischen Beispiel.
herum einschließen. Die Trajektorien werden dort
reflektiert,
was schließlich nach einigen solcher Reflexionen
dazu führt,
daß die ursprünglich auslaufende Trajektorie wieder in die Nähe
des Ursprungs zurückkehrt.
In Abbildung 3.3 zeigen wir diesen Einschlußmechanismus
an einem typischen Beispiel.
Im folgenden geben wir eine genauere Begründung dieser anschaulichen
Betrachtungen.
Dazu untersuchen wir die sich aus Gl. (3.1) ergebenden
Hamiltonschen Gleichungen:
![]()
Wir betrachten als erstes ein Teilchen
mit der Energie ![]() ,
das sich entlang der Potentialmulde
,
das sich entlang der Potentialmulde ![]() in positiver
in positiver ![]() -Richtung
bewegt und um die
-Richtung
bewegt und um die
![]() -Achse
oszilliert. Wir weisen nach, daß das Teilchen bei hinreichend
großem
-Achse
oszilliert. Wir weisen nach, daß das Teilchen bei hinreichend
großem
![]() schließlich umkehren und in das Zentrum zurücklaufen muß.
Für große
schließlich umkehren und in das Zentrum zurücklaufen muß.
Für große
![]() erhalten wir aus Gl. (3.6d):
erhalten wir aus Gl. (3.6d):
| (3.3) |
Im asymptotischen Bereich wirkt demnach auf das Teilchen eine stärkere
rücktreibende Kraft in ![]() -Richtung als durch das eindimensionale
Potential
-Richtung als durch das eindimensionale
Potential
![]() erzeugt wird. Weil aber schon
erzeugt wird. Weil aber schon ![]() zu
einer gebundenen Bewegung führt -- denn dieses Potential wächst
unbeschränkt mit
zu
einer gebundenen Bewegung führt -- denn dieses Potential wächst
unbeschränkt mit ![]() -- kann das Teilchen entlang
-- kann das Teilchen entlang ![]() in positiver
in positiver ![]() -Richtung nicht
entweichen.
Aus Symmetriegründen ist das Teilchen dann auch in negativer
-Richtung nicht
entweichen.
Aus Symmetriegründen ist das Teilchen dann auch in negativer ![]() -Richtung
gebunden.
-Richtung
gebunden.
Wir diskutieren nun die Möglichkeit eines ,,Escapes`` entlang der durch
Gl. (3.5b) beschriebenen Potentialminima
![]() .
Dabei betrachten wir zunächst nur denjenigen Ast des Minimums
.
Dabei betrachten wir zunächst nur denjenigen Ast des Minimums
![]() , der im ersten
Quadranten liegt.
Für die andere Hälfte von
, der im ersten
Quadranten liegt.
Für die andere Hälfte von ![]() und für
und für ![]() folgt dann das gleiche Resultat, wiederum wegen der Symmetrie des
Potentials.
folgt dann das gleiche Resultat, wiederum wegen der Symmetrie des
Potentials.
Für große ![]() folgt aus Gl. (3.5b)
folgt aus Gl. (3.5b)
![]() . Deshalb ist es günstig,
zu neuen Koordinaten
. Deshalb ist es günstig,
zu neuen Koordinaten 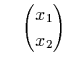 überzugehen, die aus
überzugehen, die aus ![]() durch
eine Drehung um den Winkel
durch
eine Drehung um den Winkel
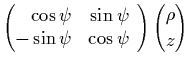 hervorgehen:
hervorgehen:
Bevor wir die kanonischen Gleichungen (3.6) in den
neuen Koordinaten auswerten, leiten wir eine für das Folgende nützliche
Abschätzung her. In der Umgebung der Nullpotentiallinie ![]() wird der zugängliche Bereich des Konfigurationsraumes -- definiert durch
die Bedingung
wird der zugängliche Bereich des Konfigurationsraumes -- definiert durch
die Bedingung
![]() -- mit zunehmendem
-- mit zunehmendem ![]() schmaler (vgl. Abbildung 3.2).
schmaler (vgl. Abbildung 3.2).
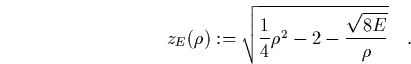 sei der größtmögliche Betrag von
sei der größtmögliche Betrag von ![]() im zugänglichen Bereich an der
Stelle
im zugänglichen Bereich an der
Stelle ![]() . Mit wachsendem
. Mit wachsendem ![]() wird
wird
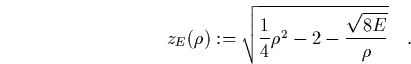 also
immer kleiner.
Um dies quantitativ zu erfassen, definieren wir als erstes
also
immer kleiner.
Um dies quantitativ zu erfassen, definieren wir als erstes
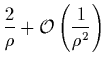 . Damit erhalten wir für
. Damit erhalten wir für
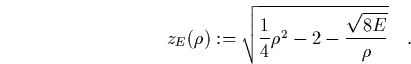 :
:
Aus Gl. (3.6) erhalten wir den folgenden Ausdruck für
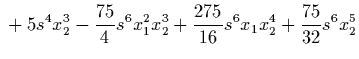 :
:
| (3.10) |
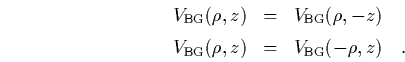 . Dies beweist schließlich, daß die
Bewegung in
. Dies beweist schließlich, daß die
Bewegung in 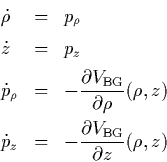 |
(3.11) |
Insgesamt haben wir damit gezeigt, daß nur auf der ![]() -Achse ein
Entweichen möglich ist. In Abbildung 3.5 demonstrieren
wir an einem typischen Orbit den gebundenen Charakter der Bewegung. Es
kann gegebenenfalls recht lange dauern, bis das Teilchen in den Kanälen
-Achse ein
Entweichen möglich ist. In Abbildung 3.5 demonstrieren
wir an einem typischen Orbit den gebundenen Charakter der Bewegung. Es
kann gegebenenfalls recht lange dauern, bis das Teilchen in den Kanälen
![]() zur Umkehr gezwungen wird.
zur Umkehr gezwungen wird.