Die in Abschnitt 3.1 vorgenommene Analyse,
insbesondere die Abbildungen 3.3 und
3.5,
deuteten schon darauf hin,
daß -- zumindest bei Energien unterhalb der Sattelpunktsenergie 16/27
-- die Dynamik in der Brown-Gabrielse-Flasche
im Zentralbereich um ![]() herum typischerweise aus der Überlagerung zweier Oszillationen besteht:
einer schnellen Oszillation in
herum typischerweise aus der Überlagerung zweier Oszillationen besteht:
einer schnellen Oszillation in ![]() -Richtung und einer viel langsameren
Oszillation in
-Richtung und einer viel langsameren
Oszillation in ![]() -Richtung. Dieses Verhalten
läßt sich damit begründen,
daß das Teilchen in
-Richtung. Dieses Verhalten
läßt sich damit begründen,
daß das Teilchen in ![]() -Richtung schon in niedrigster
(quadratischer) Ordnung gebunden ist, anders als in
-Richtung schon in niedrigster
(quadratischer) Ordnung gebunden ist, anders als in ![]() -Richtung:
-Richtung:
| (3.17) |
Es ist deshalb sinnvoll, als Poincaré-Schnittfläche
![]() die
die 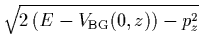 -Ebene zu
wählen.
Genauer haben wir:
-Ebene zu
wählen.
Genauer haben wir:
Die Poincaré-Abbildung ![]() ist wie gewöhnlich definiert als
die Wiederkehrabbildung für die Punkte der Poincaré-Fläche:
ist wie gewöhnlich definiert als
die Wiederkehrabbildung für die Punkte der Poincaré-Fläche:
| (3.21) |
Wir definieren hier die Poincaré-Fläche und dementsprechend die
Poincaré-Abbildung nur für Energien ![]() mit
mit
![]() .
Denn weil
.
Denn weil ![]() nicht negativ werden kann, hätte
nicht negativ werden kann, hätte ![]() zur
Folge, daß die einzigen Lösungen der kanonischen Gleichungen Fixpunkte
(im Ortsraum auf den Kurven
zur
Folge, daß die einzigen Lösungen der kanonischen Gleichungen Fixpunkte
(im Ortsraum auf den Kurven
![]() liegend) wären
-- eine triviale Situation mit relativ uninteressanter Dynamik. Die
Sattelpunktsenergie
liegend) wären
-- eine triviale Situation mit relativ uninteressanter Dynamik. Die
Sattelpunktsenergie ![]() schließen wir
aus, weil es in diesem Fall Punkte in
schließen wir
aus, weil es in diesem Fall Punkte in ![]() gibt, für die
die Wiederkehrzeit unendlich groß wird: Die beiden
Sattelpunkte
gibt, für die
die Wiederkehrzeit unendlich groß wird: Die beiden
Sattelpunkte ![]() des Potentials entsprechen dann Fixpunkten
des Potentials entsprechen dann Fixpunkten
![]() des Flusses
des Flusses ![]() .
Für größere Energien als 16/27 ist nicht mehr sichergestellt, daß
jede mit
.
Für größere Energien als 16/27 ist nicht mehr sichergestellt, daß
jede mit ![]() startende Trajektorie wieder zur Poincaré-Fläche
zurückgelangt. Auch hier sind Singularitäten, das heißt
Unstetigkeiten der Poincaré-Abbildung zu erwarten.
startende Trajektorie wieder zur Poincaré-Fläche
zurückgelangt. Auch hier sind Singularitäten, das heißt
Unstetigkeiten der Poincaré-Abbildung zu erwarten.
Zunächst ist nun zu überprüfen, ob die so definierte Abbildung ![]() die Anforderungen erfüllt, die man gewöhnlich an eine
Poincaré-Abbildung stellt. So fordert man beispielsweise, daß der
Fluß
die Anforderungen erfüllt, die man gewöhnlich an eine
Poincaré-Abbildung stellt. So fordert man beispielsweise, daß der
Fluß ![]() die Poincaré-Fläche überall transversal schneidet und
daß jeder Punkt
die Poincaré-Fläche überall transversal schneidet und
daß jeder Punkt
![]() durch den Fluß nach
endlicher Zeit
durch den Fluß nach
endlicher Zeit
![]() wieder auf
wieder auf ![]() abgebildet wird.
Die erste Bedingung stellt sicher, daß
abgebildet wird.
Die erste Bedingung stellt sicher, daß ![]() stetig und gegebenenfalls
sogar differenzierbar ist
[PaMe82]. Und nur wenn die Wiederkehrzeit
stetig und gegebenenfalls
sogar differenzierbar ist
[PaMe82]. Und nur wenn die Wiederkehrzeit
![]() für alle
für alle
![]() endlich ist, kann man sicher sein, daß die vollständige Dynamik durch
die Poincaré-Abbildung repräsentiert wird.
endlich ist, kann man sicher sein, daß die vollständige Dynamik durch
die Poincaré-Abbildung repräsentiert wird.
Um diese Eigenschaften zu überprüfen,
untersuchen wir die Radialbeschleunigung 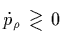 . Nach Gl. (3.6c) gilt
. Nach Gl. (3.6c) gilt
| (3.22) |
 -Werten
-Werten
Nach diesen Vorbereitungen können wir uns der numerischen Analyse der Brown-Gabrielse-Magnetflasche zuwenden und den Nachweis dafür führen, daß die Dynamik dieses Systems unter gewissen Bedingungen chaotisch ist.
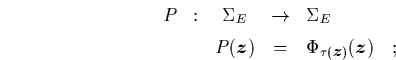 -Ebene. Auch hiermit erhielte
man eine gültige Poincaré-Abbildung mit endlichen
Wiederkehrzeiten.
Es ergäbe sich aber der für die praktische numerische
Untersuchung gravierende Nachteil, daß diese
Wiederkehrzeiten sehr viel größer wären.
-Ebene. Auch hiermit erhielte
man eine gültige Poincaré-Abbildung mit endlichen
Wiederkehrzeiten.
Es ergäbe sich aber der für die praktische numerische
Untersuchung gravierende Nachteil, daß diese
Wiederkehrzeiten sehr viel größer wären.