Der quadratische Anteil von ![]() ist
ist
Wir setzen
![]() , ausgedrückt in den neuen Koordinaten
, ausgedrückt in den neuen Koordinaten ![]() , nimmt dann die
folgende Form an:
, nimmt dann die
folgende Form an:
Wir nennen ein ![]() , dessen quadratischer Anteil die Form
(4.4) mit
, dessen quadratischer Anteil die Form
(4.4) mit ![]() hat, eine
Magnetflaschen-Hamilton-Funktion.
Selbstverständlich
bleibt aber dieser Typ von Hamilton-Funktion nicht nur den magnetischen
Flaschen vorbehalten. Die Benennung deutet lediglich an, daß die in der
Theorie der magnetischen Flaschen auftretenden Hamilton-Funktionen
typischerweise die in Gl. (4.4) beschriebene
Gestalt
annehmen --
zum Beispiel haben alle drei in Kapitel 2
vorgestellten Modellsysteme Hamilton-Funktionen dieses Typs.
Anschaulich beschreiben die ersten
hat, eine
Magnetflaschen-Hamilton-Funktion.
Selbstverständlich
bleibt aber dieser Typ von Hamilton-Funktion nicht nur den magnetischen
Flaschen vorbehalten. Die Benennung deutet lediglich an, daß die in der
Theorie der magnetischen Flaschen auftretenden Hamilton-Funktionen
typischerweise die in Gl. (4.4) beschriebene
Gestalt
annehmen --
zum Beispiel haben alle drei in Kapitel 2
vorgestellten Modellsysteme Hamilton-Funktionen dieses Typs.
Anschaulich beschreiben die ersten ![]() Summanden des
Magnetflaschen-
Summanden des
Magnetflaschen-![]() eine
(in niedrigster Ordnung) freie Bewegung, wogegen die restlichen
eine
(in niedrigster Ordnung) freie Bewegung, wogegen die restlichen 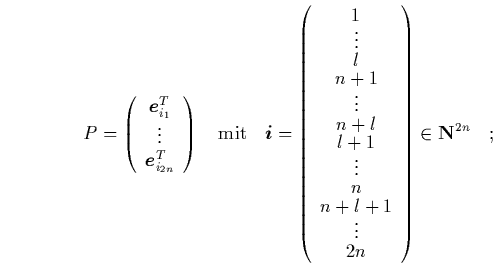 Summanden harmonische Oszillatoren mit der Frequenz
Summanden harmonische Oszillatoren mit der Frequenz ![]() darstellen.
darstellen.
Magnetflaschen-Hamilton-Funktionen können nicht mit der Gustavsonschen
Normalformentheorie untersucht werden, denn die wesentliche
Voraussetzung (1.61) ist nicht erfüllt: Um dieser
Voraussetzung zu genügen, müßte ![]() sein, und diesen Fall schließen
wir hier gerade aus.
Erst mit der DFS-Theorie wird demnach der Normalformenkalkül auf die
hier betrachtete Systemklasse anwendbar.
sein, und diesen Fall schließen
wir hier gerade aus.
Erst mit der DFS-Theorie wird demnach der Normalformenkalkül auf die
hier betrachtete Systemklasse anwendbar.
Die in den Abschnitten 1.2.2 und 1.2.3
diskutierte Transformation auf DFS-Normalform muß an dieser Stelle nicht
mehr ausführlich beschrieben werden.
Zur Erinnerung wiederholen wir hier nur diejenigen Aspekte, die sich bei
der praktischen
Durchführung
als problematisch erweisen.
Bei jedem Schritt der Normalformtransformation müssen wir
zur Lösung der homologischen Gleichung
![]() den
Grad
den
Grad ![]() -Anteil
-Anteil ![]() der Hamilton-Funktion
der Hamilton-Funktion
![]() in die
Summe
in die
Summe
![]()
Die Lie-Transformation, die die alte Hamilton-Funktion ![]() in die neue
Hamilton-Funktion
in die neue
Hamilton-Funktion ![]() transformiert, wobei
transformiert, wobei ![]() in DFS-Normalform bis zum
Grad
in DFS-Normalform bis zum
Grad ![]() ist, lautet dann
ist, lautet dann

zu bestimmenden Erzeugenden ![]() .
.
Bei der Bestimmung eines Urbildes ![]() von
von ![]() handelt es sich um ein
nichttriviales
Problem. Man hat hier zwar ,,nur`` ein lineares Gleichungssystem zu
lösen, was beispielsweise mit dem Gaußschen Eliminationsverfahren immer
gelingt, aber die Dimension des Problems ist sehr groß:
handelt es sich um ein
nichttriviales
Problem. Man hat hier zwar ,,nur`` ein lineares Gleichungssystem zu
lösen, was beispielsweise mit dem Gaußschen Eliminationsverfahren immer
gelingt, aber die Dimension des Problems ist sehr groß:
![]() . Man hat demnach Hunderte oder
sogar Tausende von linearen Gleichungen gleichzeitig zu erfüllen.
Dies stellt bis heute auch für die mächtigsten Systeme der
symbolischen Computer-Algebra ein schwieriges Problem dar,
denn die Invertierung einer
. Man hat demnach Hunderte oder
sogar Tausende von linearen Gleichungen gleichzeitig zu erfüllen.
Dies stellt bis heute auch für die mächtigsten Systeme der
symbolischen Computer-Algebra ein schwieriges Problem dar,
denn die Invertierung einer ![]() -Matrix benötigt typischerweise
-Matrix benötigt typischerweise
![]() Rechenoperationen [St89].
Andererseits wollen wir um der Rechengenauigkeit willen kein
numerisches Näherungsverfahren (Iterationsverfahren) verwenden.
Im folgenden stellen wir ein Verfahren dar, mit dem wir den Rechenaufwand
für die Invertierung von
Rechenoperationen [St89].
Andererseits wollen wir um der Rechengenauigkeit willen kein
numerisches Näherungsverfahren (Iterationsverfahren) verwenden.
Im folgenden stellen wir ein Verfahren dar, mit dem wir den Rechenaufwand
für die Invertierung von ![]() drastisch reduzieren können, indem
wir die spezielle Struktur des Problems ausnutzen und es auf ein
wesentlich einfacheres zurückführen. Damit können wir
Gl. (4.6b) vergleichsweise schnell und sehr genau
lösen und somit die Normalformtransformation durchführen.
drastisch reduzieren können, indem
wir die spezielle Struktur des Problems ausnutzen und es auf ein
wesentlich einfacheres zurückführen. Damit können wir
Gl. (4.6b) vergleichsweise schnell und sehr genau
lösen und somit die Normalformtransformation durchführen.
Für die Darstellung des Differentialoperators ![]() gemäß Gl. (1.91)
benötigen wir als erstes die Hamilton-Matrix
gemäß Gl. (1.91)
benötigen wir als erstes die Hamilton-Matrix ![]() :
:
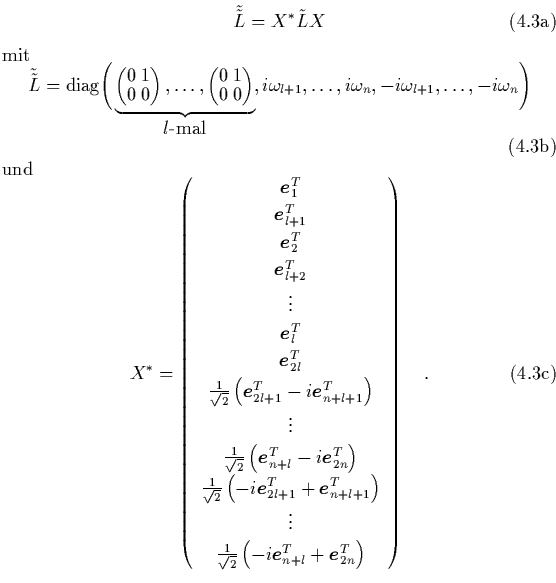 |
|||
![$\displaystyle \left(
\begin{array}{cc}
0_n&\fbox{$\displaystyle \begin{array}{@...
...cm]
0 & & \cdots & & 0 & -\omega_n
\end{array}$}& 0_n
\end{array}\right) \quad.$](img911.png) |
(4.3) |
Wir übertragen diese Idee jetzt auf die magnetischen Flaschen. Im
allgemeinen ist nicht zu erwarten, daß ![]() diagonalisierbar ist. Wir
können
diagonalisierbar ist. Wir
können ![]() aber immer in Jordansche Normalform (in ihrer komplexen
Version) überführen.
aber immer in Jordansche Normalform (in ihrer komplexen
Version) überführen. ![]() und damit auch
und damit auch ![]() werden dadurch in einem
gewissen Sinne so einfach wie möglich, so daß sich diese Transformation
als erster Schritt der Analyse anbietet.
werden dadurch in einem
gewissen Sinne so einfach wie möglich, so daß sich diese Transformation
als erster Schritt der Analyse anbietet.
Zunächst entkoppeln wir ![]() in einen Anteil, der dem Gustavsonschen
in einen Anteil, der dem Gustavsonschen
![]() entspricht (gekennzeichnet durch die Frequenzen
entspricht (gekennzeichnet durch die Frequenzen
![]() ), und in den Anteil der freien Bewegung,
der durch die
), und in den Anteil der freien Bewegung,
der durch die
![]() -Anteile der Hamilton-Funktion
beschrieben wird. Dafür verwenden wir die
-Anteile der Hamilton-Funktion
beschrieben wird. Dafür verwenden wir die ![]() -Permutationsmatrix
-Permutationsmatrix
![]() :
:
| (4.4) |
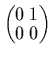 -te Zeile wird zur ersten Zeile, die
-te Zeile wird zur ersten Zeile, die 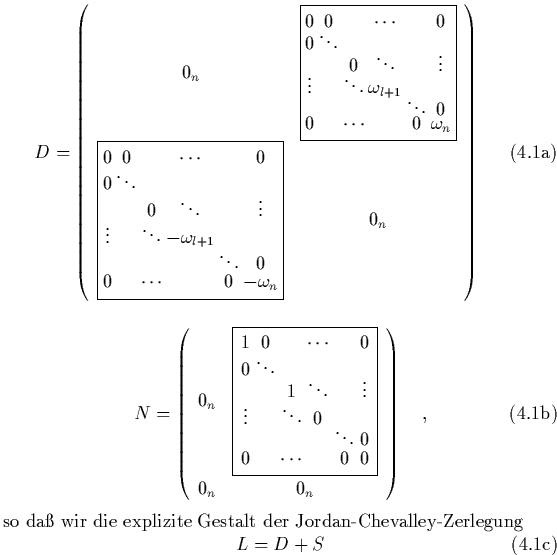 bewirkt entsprechend die Permutation der Spalten von
bewirkt entsprechend die Permutation der Spalten von
Die Anwendung von ![]() auf die Hamilton-Matrix
auf die Hamilton-Matrix ![]() ergibt:
ergibt:
![]()
Die damit erreichte Entkopplung der Anteile ![]() und
und 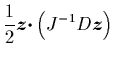 von
von 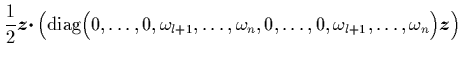 erleichtert die Jordanisierung von
erleichtert die Jordanisierung von ![]() erheblich, weil nun
beide Teilmatrizen
erheblich, weil nun
beide Teilmatrizen ![]() und
und 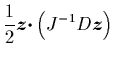 getrennt auf
Jordansche Normalform gebracht werden können.
Auf die Matrix
getrennt auf
Jordansche Normalform gebracht werden können.
Auf die Matrix ![]() muß dazu lediglich eine weitere
Zeilen- und Spaltenpermutation
angewandt werden, um die Einsen in die erste Nebendiagonale zu
verschieben.
muß dazu lediglich eine weitere
Zeilen- und Spaltenpermutation
angewandt werden, um die Einsen in die erste Nebendiagonale zu
verschieben.
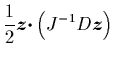 wird durch eine zu Gl. (1.73) analoge
Transformation diagonalisiert.
Wir erhalten:
wird durch eine zu Gl. (1.73) analoge
Transformation diagonalisiert.
Wir erhalten:
![\begin{subequations}
\begin{equation}
\tilde{\tilde{L}} = X^*\tilde{L}X
\end{eq...
... \right) \\ [0.1cm]
\end{array} \right) \quad.
\end{equation}\end{subequations}](img922.png)
Insgesamt gilt dann für die Jordan-Normalform der Hamilton-Matrix ![]()
![]()
die ![]() in
in
![]() überführt.
Die unitäre Matrix
überführt.
Die unitäre Matrix ![]() geht durch
Transposition und komplexe Konjugation
aus
geht durch
Transposition und komplexe Konjugation
aus ![]() hervor:
hervor: ![]() .
.
Wie Gl. (4.10b) zeigt, sind der
nilpotente Anteil von
![]() durch die Matrizen
durch die Matrizen
![]() und der diagonalisierbare Anteil durch die
Eigenwerte
und der diagonalisierbare Anteil durch die
Eigenwerte
![]() gekennzeichnet. Dementsprechend haben wir
für den diagonalisierbaren Anteil
gekennzeichnet. Dementsprechend haben wir
für den diagonalisierbaren Anteil ![]() und den nilpotenten Anteil
und den nilpotenten Anteil ![]() von
von
![]() :
:
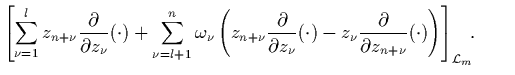
gefunden haben.
Mit Gl. (4.12a) ist dann auch der Nachweis erbracht,
daß das von Dragt und Finn gefundene 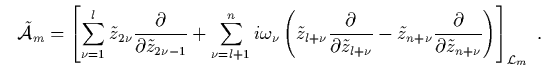 (siehe Gl. (1.106)) wirklich ein
Integral der Bewegung für in DFS-Normalform befindliche
Magnetflaschen-Hamilton-Funktionen ist, denn es gilt:
(siehe Gl. (1.106)) wirklich ein
Integral der Bewegung für in DFS-Normalform befindliche
Magnetflaschen-Hamilton-Funktionen ist, denn es gilt:
| (4.2) |
Wenn man lediglich an dem Integral der Bewegung für Magnetflaschen
interessiert wäre, dann wären die oben dargestellten langwierigen
Umformungen
unnötig, denn einerseits kann man der Matrix 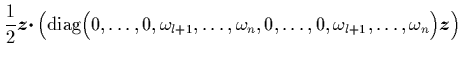 schon fast ,,ansehen``, wie ihr diagonalisierbarer Anteil beschaffen ist
-- auf diese Weise wird das Integral
schon fast ,,ansehen``, wie ihr diagonalisierbarer Anteil beschaffen ist
-- auf diese Weise wird das Integral 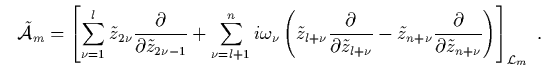 beispielsweise
in [St91] gefunden. Andererseits könnte man auch die Ergebnisse
des Anhanges A
anwenden und damit
beispielsweise
in [St91] gefunden. Andererseits könnte man auch die Ergebnisse
des Anhanges A
anwenden und damit ![]() sofort aus der Hamilton-Funktion (4.4) ablesen,
ohne
sofort aus der Hamilton-Funktion (4.4) ablesen,
ohne ![]() überhaupt berechnen zu müssen.
überhaupt berechnen zu müssen.
Unabhängig von der Bestimmung des DFS-Integrals ist aber die durch ![]() gegebene Koordinatentransformation ein nützliches Hilfsmittel für die
Invertierung von
gegebene Koordinatentransformation ein nützliches Hilfsmittel für die
Invertierung von ![]() , die für die Lösung von Gl. (4.6b) benötigt wird. Dies wird deutlich, wenn man die
Transformation
, die für die Lösung von Gl. (4.6b) benötigt wird. Dies wird deutlich, wenn man die
Transformation
Wir notieren ![]() zunächst in den alten Koordinaten
zunächst in den alten Koordinaten
![]() :
:
| (4.5) |
![[*]](crossref.png) anhand eines
Beispiels genauer auf diese Eigenschaft von
anhand eines
Beispiels genauer auf diese Eigenschaft von
Um uns ein genaueres Bild von der Wirkungsweise von
![]() zu
verschaffen, wenden wir den Operator auf einen der Basisvektoren
zu
verschaffen, wenden wir den Operator auf einen der Basisvektoren
![]() von
von ![]() an:
an:
Bevor wir
![]() weiter analysieren können, müssen wir noch
festlegen, in welcher Reihenfolge die Monome
weiter analysieren können, müssen wir noch
festlegen, in welcher Reihenfolge die Monome
![]() den kanonischen Basisvektoren des
den kanonischen Basisvektoren des ![]() zugeordnet werden. Wir
können diese Zuordnung beliebig
wählen. Dabei ist zu beachten, daß eine geeignete Zuordnung die
Matrixdarstellung von
zugeordnet werden. Wir
können diese Zuordnung beliebig
wählen. Dabei ist zu beachten, daß eine geeignete Zuordnung die
Matrixdarstellung von
![]() entscheidend vereinfachen kann.
Aus [Gu66] ist die Gustavson-Anordnung der Monome
entscheidend vereinfachen kann.
Aus [Gu66] ist die Gustavson-Anordnung der Monome
![]() bekannt:
bekannt:
![]() bekommt den Gustavson-Index
bekommt den Gustavson-Index
![]() .
Für
.
Für
![]() definiert man
definiert man
![]() , wenn es ein
, wenn es ein ![]() gibt,
so daß
gibt,
so daß
![]() und
und ![]() für alle
für alle  gilt.
Mit dieser Abbildungsvorschrift erhält man einen bijektiven Zusammenhang
zwischen den Monomen
gilt.
Mit dieser Abbildungsvorschrift erhält man einen bijektiven Zusammenhang
zwischen den Monomen
![]() aus
aus ![]() und den
natürlichen Zahlen
und den
natürlichen Zahlen
![]() .
Für die
Monome vom Grad
.
Für die
Monome vom Grad  haben wir diese Zuordnung in Tabelle
4.1 angegeben. (Außer dem Gustavson-Index
haben wir diese Zuordnung in Tabelle
4.1 angegeben. (Außer dem Gustavson-Index ![]() ist dort
auch der ,,Magnetflaschenindex``
ist dort
auch der ,,Magnetflaschenindex`` ![]() tabelliert, den wir weiter
unten einführen werden.)
tabelliert, den wir weiter
unten einführen werden.)
|
|
Mit den Gustavson-Indizes ist dann eine Anordnung der Monome in ![]() gegeben, die wir zum Beispiel verwenden können, um
gegeben, die wir zum Beispiel verwenden können, um
![]() in
Matrixgestalt zu schreiben.
Als ein Beispiel geben wir die Matrixdarstellung von
in
Matrixgestalt zu schreiben.
Als ein Beispiel geben wir die Matrixdarstellung von
![]() im Fall
im Fall ![]() ,
, ![]() an. Für diesen Wert von
an. Für diesen Wert von ![]() ist
ist
![]() . Wir verwenden hier die Abkürzung
. Wir verwenden hier die Abkürzung
![]() und schreiben Nullen, die nicht auf der Diagonalen
liegen, nicht aus:
und schreiben Nullen, die nicht auf der Diagonalen
liegen, nicht aus:
Darüber hinaus ist
![]() für alle
für alle ![]() ,
, ![]() und
und ![]() eine rechte
obere Dreiecksmatrix, wenn
man die Gustavsonsche Monom-Indizierung zugrunde legt.
Man erkennt diese Eigenschaft anhand von Gl. (4.18). Der
zweite Summand in dieser Gleichung ergibt einen Beitrag auf der
Diagonalen von
eine rechte
obere Dreiecksmatrix, wenn
man die Gustavsonsche Monom-Indizierung zugrunde legt.
Man erkennt diese Eigenschaft anhand von Gl. (4.18). Der
zweite Summand in dieser Gleichung ergibt einen Beitrag auf der
Diagonalen von
![]() , wie wir schon früher
erkannt haben. Der erste Summand führt auf Beiträge der Form
, wie wir schon früher
erkannt haben. Der erste Summand führt auf Beiträge der Form
Obwohl demnach
![]() eine Dreiecksmatrix ist, können wir das
lineare Gleichungssystem (4.6b) nicht einfach
durch gewöhnliches Rückwärtseinsetzen lösen, indem wir zuerst die
eine Dreiecksmatrix ist, können wir das
lineare Gleichungssystem (4.6b) nicht einfach
durch gewöhnliches Rückwärtseinsetzen lösen, indem wir zuerst die
![]() -te Gleichung
lösen, dann die
-te Gleichung
lösen, dann die ![]() -te usw. Denn die Diagonalelemente der Matrix
sind nicht sämtlich von null verschieden, was während des
Rückwärtseinsetzens
dazu führt, daß man einige Komponenten des Lösungsvektors wählen
muß. Erst bei nachfolgenden Schritten des Verfahrens erweist sich dann,
ob diese Wahl sinnvoll war oder zu Widersprüchen
führt4.1.
Es kann also a priori kein konsistentes Lösungsverfahren für eine Matrix
der hier vorliegenden Form angegeben werden, wenn man nicht wie beim
Gaußschen Verfahren eliminieren möchte. Dies wollen wir wegen des
erforderlichen großen Aufwandes aber gerade vermeiden.
-te usw. Denn die Diagonalelemente der Matrix
sind nicht sämtlich von null verschieden, was während des
Rückwärtseinsetzens
dazu führt, daß man einige Komponenten des Lösungsvektors wählen
muß. Erst bei nachfolgenden Schritten des Verfahrens erweist sich dann,
ob diese Wahl sinnvoll war oder zu Widersprüchen
führt4.1.
Es kann also a priori kein konsistentes Lösungsverfahren für eine Matrix
der hier vorliegenden Form angegeben werden, wenn man nicht wie beim
Gaußschen Verfahren eliminieren möchte. Dies wollen wir wegen des
erforderlichen großen Aufwandes aber gerade vermeiden.
Die Lösung des Problems gelingt durch die Einführung einer anderen
Anordnung der Monome von ![]() . Wir nennen diese Variation der
Gustavsonschen Zuordnung die Magnetflaschenanordnung der Monome
von
. Wir nennen diese Variation der
Gustavsonschen Zuordnung die Magnetflaschenanordnung der Monome
von ![]() , weil sie dem Operator
, weil sie dem Operator
![]() , der sich aus einer
Magnetflaschen-Hamilton-Funktion ergibt, angepaßt ist.
, der sich aus einer
Magnetflaschen-Hamilton-Funktion ergibt, angepaßt ist.
Die dem Folgenden zugrunde liegende Idee besteht darin, daß die Lösung
einer
linearen Gleichung
 einfach und mit geringem
Aufwand gelingt, wenn die einzigen
von null verschiedenen Einträge der
einfach und mit geringem
Aufwand gelingt, wenn die einzigen
von null verschiedenen Einträge der ![]() -Matrix
-Matrix
![]() auf der Haupt- und der ersten oberen Nebendiagonalen liegen.
In diesem Fall kann man
die einzelnen Gleichungen durch ein
dem Rückwärtseinsetzen ähnliches Verfahren mit sehr wenigen
(nämlich
auf der Haupt- und der ersten oberen Nebendiagonalen liegen.
In diesem Fall kann man
die einzelnen Gleichungen durch ein
dem Rückwärtseinsetzen ähnliches Verfahren mit sehr wenigen
(nämlich ![]() ) Rechenoperationen lösen, ohne daß dabei
Inkonsistenzen auftreten können. Wir gehen hier nicht näher auf dieses
Verfahren ein, denn obwohl es sehr einfach ist, wäre seine Darstellung
an dieser Stelle wenig instruktiv.
Wie wir sehen werden, nimmt
) Rechenoperationen lösen, ohne daß dabei
Inkonsistenzen auftreten können. Wir gehen hier nicht näher auf dieses
Verfahren ein, denn obwohl es sehr einfach ist, wäre seine Darstellung
an dieser Stelle wenig instruktiv.
Wie wir sehen werden, nimmt
![]() für die Magnetflaschenanordnung der Monome
für die Magnetflaschenanordnung der Monome
![]() die beschriebene Gestalt an, so daß wir das Problem der
Invertierung von
die beschriebene Gestalt an, so daß wir das Problem der
Invertierung von ![]() bzw. der Lösung von Gl. (4.6b) einfach und schnell lösen können.
bzw. der Lösung von Gl. (4.6b) einfach und schnell lösen können.
Diese Vorgehensweise hat allerdings den Nachteil,
daß wir uns bei der Einführung
der Magnetflaschen-Anordnung auf den Fall ![]() beschränken müssen.
Für
beschränken müssen.
Für ![]() erhalten wir aus Gl. (4.18)
erhalten wir aus Gl. (4.18)
| (4.8) |
| (4.9) |
Auf diese Weise erhält man eine gegenüber Gustavson
abgewandelte Anordnung der Monome. Der Zusammenhang zwischen
![]() und
und ![]() ist bijektiv, wie wir es zu
fordern haben. Man vergleiche Tabelle 4.1 für eine
Gegenüberstellung der
ist bijektiv, wie wir es zu
fordern haben. Man vergleiche Tabelle 4.1 für eine
Gegenüberstellung der ![]() - und
- und ![]() -Indizes der Monome vom Grad
0 bis 4.
-Indizes der Monome vom Grad
0 bis 4.
Wie wir es beabsichtigt haben, liegt
die Wirkung der zusätzlich eingeführten Regel 2b
darin, daß bei Verwendung der Magnetflaschenanordnung alle
Außerdiagonalelemente von
![]() auf der ersten oberen
Nebendiagonalen zu liegen kommen.
Wir demonstrieren diese Eigenschaft wiederum anhand von
auf der ersten oberen
Nebendiagonalen zu liegen kommen.
Wir demonstrieren diese Eigenschaft wiederum anhand von
![]() .
Bei Verwendung der Magnetflaschenindizes gilt:
.
Bei Verwendung der Magnetflaschenindizes gilt:
Mit dem in dieser Gestalt vorliegenden
![]() ist es nun
vergleichsweise einfach, die für die Normalformtransformation
entscheidende Gl. (4.6b) zu lösen und die Erzeugende
ist es nun
vergleichsweise einfach, die für die Normalformtransformation
entscheidende Gl. (4.6b) zu lösen und die Erzeugende
![]() zu bestimmen.
Darüber hinaus bietet die Darstellung von
zu bestimmen.
Darüber hinaus bietet die Darstellung von
![]() mittels der
Magnetflaschenanordnung
noch in einer anderen Hinsicht
einen wesentlichen Vorteil:
In dieser
Darstellung ist es besonders einfach, eine Basis der Untervektorräume
mittels der
Magnetflaschenanordnung
noch in einer anderen Hinsicht
einen wesentlichen Vorteil:
In dieser
Darstellung ist es besonders einfach, eine Basis der Untervektorräume
![]() und
und
![]() zu
berechnen4.2.
Wir benötigen diese
Basen, um den Grad
zu
berechnen4.2.
Wir benötigen diese
Basen, um den Grad ![]() -Anteil
-Anteil ![]() der Hamilton-Funktion gemäß Gl. (4.5) aufspalten zu können -- eine unabdingbare
Voraussetzung für die Aufstellung und Lösung der homologischen
Gleichung.
der Hamilton-Funktion gemäß Gl. (4.5) aufspalten zu können -- eine unabdingbare
Voraussetzung für die Aufstellung und Lösung der homologischen
Gleichung.
Wir haben jetzt die für eine effiziente Normalisierung von
![]() benötigten Hilfsmittel bereitgestellt.
Wir merken an dieser Stelle noch einmal an, daß der Durchführung der
Normalformtransformation auch dann nichts im Wege steht, wenn die
in diesem Abschnitt gemachten Annahmen (Magnetflaschen-Hamilton-Funktion,
benötigten Hilfsmittel bereitgestellt.
Wir merken an dieser Stelle noch einmal an, daß der Durchführung der
Normalformtransformation auch dann nichts im Wege steht, wenn die
in diesem Abschnitt gemachten Annahmen (Magnetflaschen-Hamilton-Funktion,
![]() ) nicht zutreffen. Man muß dann aber, bedingt durch die hohe
Dimension von
) nicht zutreffen. Man muß dann aber, bedingt durch die hohe
Dimension von ![]() , großen numerischen Aufwand in Kauf nehmen, den
wir hier vermeiden konnten.
, großen numerischen Aufwand in Kauf nehmen, den
wir hier vermeiden konnten.
Schließlich stellen wir fest, daß die in diesem Abschnitt besprochene
Problematik im Fall der Gustavsonschen Normalform irrelevant ist. Das
Gustavsonsche ![]() stellt den Grenzfall des Magnetflaschen-
stellt den Grenzfall des Magnetflaschen-![]() mit
mit
![]() dar. Wenn
dar. Wenn ![]() ist, dann ist
ist, dann ist
![]() schon diagonal, wie wir
in Abschnitt 1.2.2 gesehen haben. Sowohl die
Invertierung von
schon diagonal, wie wir
in Abschnitt 1.2.2 gesehen haben. Sowohl die
Invertierung von
![]() als auch die Zerlegung von
als auch die Zerlegung von ![]() in
Kern- und Bildvektorraum von
in
Kern- und Bildvektorraum von ![]() sind dann vergleichsweise triviale
Aufgaben. Man vergleiche hierzu die Gln. (1.79) und (1.80).
sind dann vergleichsweise triviale
Aufgaben. Man vergleiche hierzu die Gln. (1.79) und (1.80).