Für das Folgende sind die Gln. (1.95) und
(1.108) von entscheidender Bedeutung. Sie geben
explizite Formeln an für eine beliebige quadratische Hamilton-Funktion
![]() bzw. für das entsprechende zweite Integral
bzw. für das entsprechende zweite Integral ![]() der
DFS-Theorie. Sowohl
der
DFS-Theorie. Sowohl ![]() als auch
als auch ![]() hängen nur von der
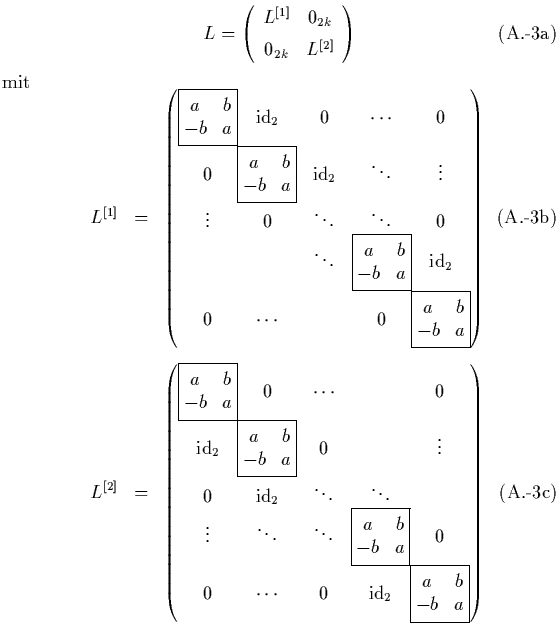
Hamilton-Matrix
hängen nur von der
Hamilton-Matrix ![]() ab. Zur Erinnerung: nach Gl. (1.34)
gilt für die Hamilton-Matrix:
ab. Zur Erinnerung: nach Gl. (1.34)
gilt für die Hamilton-Matrix:
![]() .
Die einzige Einschränkung, die wir an dieser Stelle machen, ist die
Forderung, daß die Hamilton-Funktion und damit auch
.
Die einzige Einschränkung, die wir an dieser Stelle machen, ist die
Forderung, daß die Hamilton-Funktion und damit auch ![]() reell sein
sollenA.2.
Demnach ist die Klassifizierung aller
reell sein
sollenA.2.
Demnach ist die Klassifizierung aller ![]() gleichbedeutend mit
der Klassifizierung der reellen Matrizen
gleichbedeutend mit
der Klassifizierung der reellen Matrizen ![]() .
.
Jede ![]() -Matrix kann mittels einer
Ähnlichkeitstransformation auf
Jordansche Normalform transformiert werden. Wir beschränken uns hier,
anders als in Gl. (1.2), auf die reelle Version dieses
Satzes, die man beispielsweise in [ArPl90] findet: Die
reelle Matrix
-Matrix kann mittels einer
Ähnlichkeitstransformation auf
Jordansche Normalform transformiert werden. Wir beschränken uns hier,
anders als in Gl. (1.2), auf die reelle Version dieses
Satzes, die man beispielsweise in [ArPl90] findet: Die
reelle Matrix ![]() kann durch eine Ähnlichkeitstransformation
mit einer
orthogonalen (also insbesondere ebenfalls reellen)
Transformationsmatrix
kann durch eine Ähnlichkeitstransformation
mit einer
orthogonalen (also insbesondere ebenfalls reellen)
Transformationsmatrix
![]() in die folgende Gestalt gebracht werden:
in die folgende Gestalt gebracht werden:
![]()
(
![]() ) gilt.
Im Fall eines Jordan-Blockes vom Typ (A.1b)
ist
) gilt.
Im Fall eines Jordan-Blockes vom Typ (A.1b)
ist ![]() ein reeller Eigenwert von
ein reeller Eigenwert von 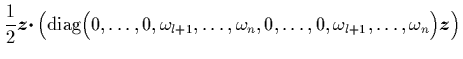 , während ein
Jordan-Block vom Typ (A.1c) einem
komplex-konjugierten Eigenwertpaar
, während ein
Jordan-Block vom Typ (A.1c) einem
komplex-konjugierten Eigenwertpaar  entspricht.
Wir verwenden die Jordan-Normalform hier in ihrer reellen Form, damit wir
als Resultat unserer Untersuchungen wieder reelle
entspricht.
Wir verwenden die Jordan-Normalform hier in ihrer reellen Form, damit wir
als Resultat unserer Untersuchungen wieder reelle ![]() und
reelle Integrale
und
reelle Integrale ![]() erhalten.
erhalten.
Wir gehen von nun an davon aus,
daß ![]() in reeller Jordanscher Normalform
vorliegt. Diese zusätzliche Annahme vereinfacht die Darstellung der
folgenden Sachverhalte erheblich, ist aber nicht prinzipiell notwendig.
Wir merken hierzu lediglich an, daß Komplikationen für eine nicht in
Normalform befindliche Hamilton-Matrix
in reeller Jordanscher Normalform
vorliegt. Diese zusätzliche Annahme vereinfacht die Darstellung der
folgenden Sachverhalte erheblich, ist aber nicht prinzipiell notwendig.
Wir merken hierzu lediglich an, daß Komplikationen für eine nicht in
Normalform befindliche Hamilton-Matrix ![]() dadurch entstehen
können, daß die
Koordinatentransformation
dadurch entstehen
können, daß die
Koordinatentransformation
![]() , mit der
man
, mit der
man ![]() in die Gestalt
in die Gestalt
![]() der Gl. (A.1) bringt, in der Regel nicht kanonisch ist.
Da dieser Abschnitt A.1 aber lediglich der Motivation der
Galinschen Vorgehensweise dient, müssen wir hier nicht notwendigerweise
eine vollständige Beschreibung geben. In der allgemeinen, in Abschnitt
A.2 vorgestellten Theorie ist eine entsprechende
Forderung an
der Gl. (A.1) bringt, in der Regel nicht kanonisch ist.
Da dieser Abschnitt A.1 aber lediglich der Motivation der
Galinschen Vorgehensweise dient, müssen wir hier nicht notwendigerweise
eine vollständige Beschreibung geben. In der allgemeinen, in Abschnitt
A.2 vorgestellten Theorie ist eine entsprechende
Forderung an ![]() nicht notwendig.
nicht notwendig.
Ausgehend von einer Hamilton-Funktion
![]() , die sich
in DFS-Normalform
befindetA.3und deren Hamilton-Matrix gemäß Gl. (A.1) in
Jordan-Normalform vorliegt,
bestimmen wir jetzt die zweiten Integrale der Bewegung im Fall
zweier Freiheitsgrade der Bewegung (
, die sich
in DFS-Normalform
befindetA.3und deren Hamilton-Matrix gemäß Gl. (A.1) in
Jordan-Normalform vorliegt,
bestimmen wir jetzt die zweiten Integrale der Bewegung im Fall
zweier Freiheitsgrade der Bewegung (![]() ).
Wir nutzen die Tatsache aus, daß das Eigenwertspektrum von
).
Wir nutzen die Tatsache aus, daß das Eigenwertspektrum von ![]() zwei wichtigen Bedingungen unterliegt. Zum einen treten Eigenwerte von
zwei wichtigen Bedingungen unterliegt. Zum einen treten Eigenwerte von
![]() , die nicht rein reell sind, immer als komplex-konjugierte Paare
, die nicht rein reell sind, immer als komplex-konjugierte Paare
![]() auf,
weil
auf,
weil ![]() reell ist. Zum anderen ist mit
reell ist. Zum anderen ist mit 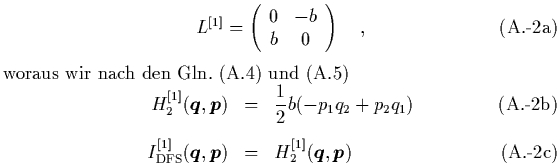 auch
auch  ein
Eigenwert von
ein
Eigenwert von ![]() , wie wir schon in Abschnitt 1.1.2
gezeigt haben.
Damit sind die folgenden Eigenwerttupel von
, wie wir schon in Abschnitt 1.1.2
gezeigt haben.
Damit sind die folgenden Eigenwerttupel von ![]() möglich:
Quadrupel
möglich:
Quadrupel 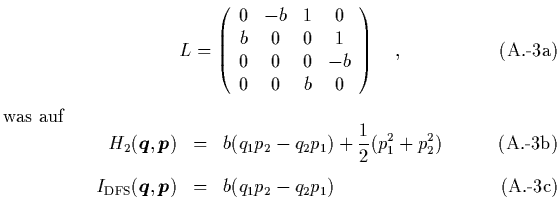 , Paare
, Paare 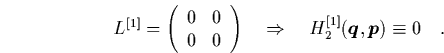 und
und ![]() sowie 0.
sowie 0. ![]() und
und 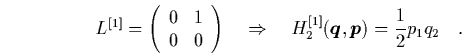 sind hier von null verschiedene reelle Zahlen.
sind hier von null verschiedene reelle Zahlen.
Es ergeben sich die nachfolgend aufgeführten Möglichkeiten für die
Eigenwerte 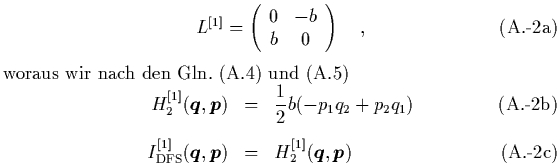 der
der 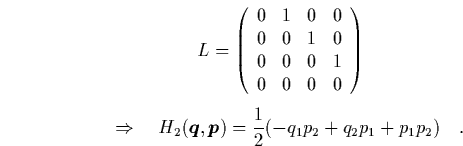 -Matrix
-Matrix ![]() und entsprechend für die
jeweiligen Integrale der Bewegung
und entsprechend für die
jeweiligen Integrale der Bewegung ![]() :
:
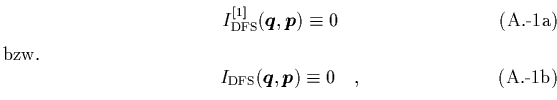 .
In diesem Fall erhalten wir für
.
In diesem Fall erhalten wir für 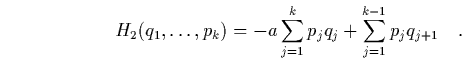 auftritt, sind zwei
unterschiedliche Fälle möglich:
auftritt, sind zwei
unterschiedliche Fälle möglich:
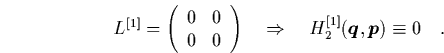 haben jeweils die
algebraische Vielfachheit eins (als Nullstelle des
charakteristischen Polynoms von
haben jeweils die
algebraische Vielfachheit eins (als Nullstelle des
charakteristischen Polynoms von 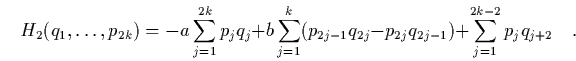 -Matrix
-Matrix
![$L^{[2]}$](img1145.png) .
Wegen der Blockgestalt von
.
Wegen der Blockgestalt von ![\begin{subequations}
\begin{equation}
I_{\rm DFS}({\mbox{\protect\boldmath$q$}...
...$}D^{[2]}{\mbox{\protect\boldmath$p$}} \quad,
\end{eqnarray} \end{subequations}](img1147.png)
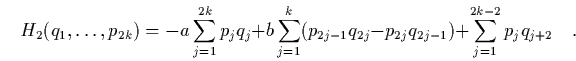 -Matrizen
-Matrizen ![$D^{[i]},i=1,2$](img1148.png) aus den
entsprechenden Zerlegungen
aus den
entsprechenden Zerlegungen
![$L^{[i]}=D^{[i]}+N^{[i]}$](img1149.png) in den diagonalisierbaren und den nilpotenten Anteil
ergeben.
in den diagonalisierbaren und den nilpotenten Anteil
ergeben.
Für das Eigenwertpaar 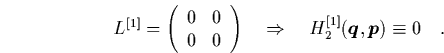 der Matrix
der Matrix ![]() erhalten wir also die folgenden Beiträge zur
Hamilton-Funktion bzw. zum DFS-Integral:
erhalten wir also die folgenden Beiträge zur
Hamilton-Funktion bzw. zum DFS-Integral:
 |
(A.-2) | ||
![$\displaystyle H_2^{[1]}({\mbox{\protect\boldmath$q$}},{\mbox{\protect\boldmath$p$}}) \quad,$](img1154.png) |
(A.-1) |
Die jeweils anderen Beiträge ![$H_2^{[2]}$](img1156.png) und
und
![$I_{\rm DFS}^{[2]}$](img1157.png) hängen noch von der
Eigenwertstruktur des zweiten Jordankästchens
hängen noch von der
Eigenwertstruktur des zweiten Jordankästchens ![$L^{[2]}$](img1145.png) ab, über das wir unter diesem Punkt keine Aussage machen
wollen.
ab, über das wir unter diesem Punkt keine Aussage machen
wollen.
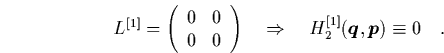 nichttriviale Jordan-Kästchen entsprechen,
nichttriviale Jordan-Kästchen entsprechen,
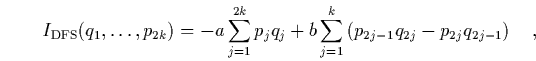 ist, wie
man Gl. (A.8a) unmittelbar entnimmt.
ist, wie
man Gl. (A.8a) unmittelbar entnimmt.
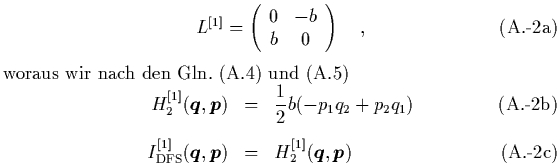 rein imaginär ist, gibt es das Eigenwertpaar
rein imaginär ist, gibt es das Eigenwertpaar
![$L^{[2]}$](img1145.png) gilt, ist die Situation keineswegs
trivial, denn sie bedeutet nicht
etwa, daß die gesamte Hamilton-Funktion identisch null
ist. Lediglich der Term niedrigster Ordnung von
gilt, ist die Situation keineswegs
trivial, denn sie bedeutet nicht
etwa, daß die gesamte Hamilton-Funktion identisch null
ist. Lediglich der Term niedrigster Ordnung von
| (A.-2) |
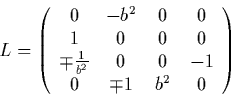 |
(A.-1) |
![$[1]$](img1169.png) -Komponente sind in allen drei Fällen null:
-Komponente sind in allen drei Fällen null:
Mit dieser Auflistung haben wir alle für ![]() möglichen
Eigenwertkonstellationen von
möglichen
Eigenwertkonstellationen von ![]() erfaßt.
Es sei noch explizit darauf hingewiesen, daß man zwei beliebige
der Fälle 2a, 3a,
4a und 4b gemäß Gl. (A.3) kombinieren kann, um die
Hamilton-Matrix
erfaßt.
Es sei noch explizit darauf hingewiesen, daß man zwei beliebige
der Fälle 2a, 3a,
4a und 4b gemäß Gl. (A.3) kombinieren kann, um die
Hamilton-Matrix ![]() vollständig zu charakterisieren. Man erhält dann
vollständig zu charakterisieren. Man erhält dann
![]() und
und ![]() wieder aus den Gln. (A.4) und
(A.5).
wieder aus den Gln. (A.4) und
(A.5).
Damit ist für ![]() die vollständige Auflistung aller ,,irreduziblen``
Hamilton-Funktionen aus
die vollständige Auflistung aller ,,irreduziblen``
Hamilton-Funktionen aus ![]() mitsamt den durch sie definierten
DFS-Integralen abgeschlossen.
Eine wichtige Folgerung ergibt sich insbesondere aus der Gestalt von
mitsamt den durch sie definierten
DFS-Integralen abgeschlossen.
Eine wichtige Folgerung ergibt sich insbesondere aus der Gestalt von
![]() in Punkt 4: Zwar kann man, wie in
Stegemertens Satz 1.4 zutreffend festgestellt wird,
jede Hamilton-Funktion auf DFS-Normalform transformieren und dann mit
deren Hilfe ein zweites Integral der Bewegung
in Punkt 4: Zwar kann man, wie in
Stegemertens Satz 1.4 zutreffend festgestellt wird,
jede Hamilton-Funktion auf DFS-Normalform transformieren und dann mit
deren Hilfe ein zweites Integral der Bewegung ![]() bestimmen.
Wenn aber alle Eigenwerte der Hamilton-Matrix
bestimmen.
Wenn aber alle Eigenwerte der Hamilton-Matrix ![]() null sind, dann ist
dieses neue Integral identisch null und ergibt keine neue Information
über das System!
null sind, dann ist
dieses neue Integral identisch null und ergibt keine neue Information
über das System!
Darüber hinaus ergibt sich aus dem formalen Charakter (vergleiche
Kapitel 1) eine weitere wichtige Bemerkung. Selbst wenn
man ein von null verschiedenes formales zweites Integral ![]() konstruieren kann, heißt dies noch nicht, daß
konstruieren kann, heißt dies noch nicht, daß ![]() ein
echtes Integral der Bewegung ist: Über die Konvergenz der das
Integral darstellenden Potenzreihe können wir keine allgemeine Aussage
machen.
ein
echtes Integral der Bewegung ist: Über die Konvergenz der das
Integral darstellenden Potenzreihe können wir keine allgemeine Aussage
machen.
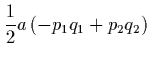 hervor, denn in Gl. (1.34) ist
hervor, denn in Gl. (1.34) ist
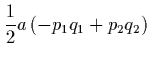 , wenn man
, wenn man