Nach Galin [Ar89, Anhang 6] ist die folgende Liste (Gln. (A.15),...,(A.20)) von sechs
quadratischen Hamilton-Funktionen ![]() vollständig:
Alle anderen quadratischen Hamilton-Funktionen erhält
man dadurch, daß man mehrere
der folgenden
vollständig:
Alle anderen quadratischen Hamilton-Funktionen erhält
man dadurch, daß man mehrere
der folgenden ![]() linear kombiniert -- so wie wir es in Gl. (A.4) an einem einfachen Beispiel demonstriert haben -- und
die so erhaltene Hamilton-Funktion einer geeigneten linearen kanonischen
Transformation unterwirft.
Die im folgenden aufgeführten sechs
linear kombiniert -- so wie wir es in Gl. (A.4) an einem einfachen Beispiel demonstriert haben -- und
die so erhaltene Hamilton-Funktion einer geeigneten linearen kanonischen
Transformation unterwirft.
Die im folgenden aufgeführten sechs ![]() -Typen werden deshalb als die
Normalformen der quadratischen Hamilton-Funktionen bezeichnet.
-Typen werden deshalb als die
Normalformen der quadratischen Hamilton-Funktionen bezeichnet.
Die Galinsche Klassifizierung wird in konsequenter Verallgemeinerung
unseres Vorgehens in Abschnitt A.1 konstruiert. Ausgehend
von der speziellen Eigenwertstruktur der Hamilton-Matrix (siehe Seite
![[*]](crossref.png) ) , werden
systematisch diejenigen Hamilton-Funktionen aufgelistet, die den
für eine Hamilton-Matrix möglichen Eigenwerttupeln
entsprechen, wobei die jeweils erlaubten Dimensionen
des Jordan-Kästchens dieses Eigenwerttupels berücksichtigt werden.
) , werden
systematisch diejenigen Hamilton-Funktionen aufgelistet, die den
für eine Hamilton-Matrix möglichen Eigenwerttupeln
entsprechen, wobei die jeweils erlaubten Dimensionen
des Jordan-Kästchens dieses Eigenwerttupels berücksichtigt werden.
Wir weisen an dieser Stelle noch darauf hin, daß sich die
Hamilton-Funktionen für ![]() , die man durch Linearkombination der
Normalformen dieses Abschnittes erhält, von den in Abschnitt
A.1 diskutierten Hamilton-Funktionen teilweise
unterscheiden, was jeweils auf eine andere Anordnung der Zeilen und
Spalten in den Hamilton-Matrizen zurückzuführen ist. Wir müssen uns
hier auf Galins Aussage verlassen, daß alle Hamilton-Funktionen
nach dem oben genannten Schema aus seinen Normalformen hergeleitet werden
können.
, die man durch Linearkombination der
Normalformen dieses Abschnittes erhält, von den in Abschnitt
A.1 diskutierten Hamilton-Funktionen teilweise
unterscheiden, was jeweils auf eine andere Anordnung der Zeilen und
Spalten in den Hamilton-Matrizen zurückzuführen ist. Wir müssen uns
hier auf Galins Aussage verlassen, daß alle Hamilton-Funktionen
nach dem oben genannten Schema aus seinen Normalformen hergeleitet werden
können.
 , die jeweils einen
Jordan-Block der Dimension
, die jeweils einen
Jordan-Block der Dimension  entsprechen, gilt:
entsprechen, gilt:
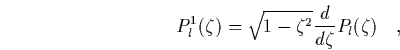
Wir nun die Galinschen Normalformen für quadratische Hamilton-Funktionen und den Normalformbegriff der Dragt-Finn-Stegemerten-Theorie kombinieren und die folgende Definition einer verallgemeinerten Normalform geben.
Diese Definition ist sinnvoll, denn jede Hamilton-Funktion ![]() kann
im Sinn von Definition A.1 normalisiert werden: Nach Galin
kann jedes
kann
im Sinn von Definition A.1 normalisiert werden: Nach Galin
kann jedes ![]() kanonisch in eine Linearkombination von
kanonisch in eine Linearkombination von ![]() -Termen der
Typen I bis
VI transformiert werden, und Stegemertens Satz 1.3
stellt die Normalisierbarkeit der Anteile von
-Termen der
Typen I bis
VI transformiert werden, und Stegemertens Satz 1.3
stellt die Normalisierbarkeit der Anteile von ![]() mit größerem Grad als
zwei sicher.
Die Diskussion von in verallgemeinerter Normalform befindlichen
Hamilton-Funktionen bietet sich deswegen an, weil man für diese
Hamilton-Funktionen (bis auf eine Ausnahme) unmittelbar die zweiten
Integrale der DFS-Theorie angeben kann, ebenso wie das in Abschnitt
A.1 für den Fall
mit größerem Grad als
zwei sicher.
Die Diskussion von in verallgemeinerter Normalform befindlichen
Hamilton-Funktionen bietet sich deswegen an, weil man für diese
Hamilton-Funktionen (bis auf eine Ausnahme) unmittelbar die zweiten
Integrale der DFS-Theorie angeben kann, ebenso wie das in Abschnitt
A.1 für den Fall ![]() gelang.
gelang.
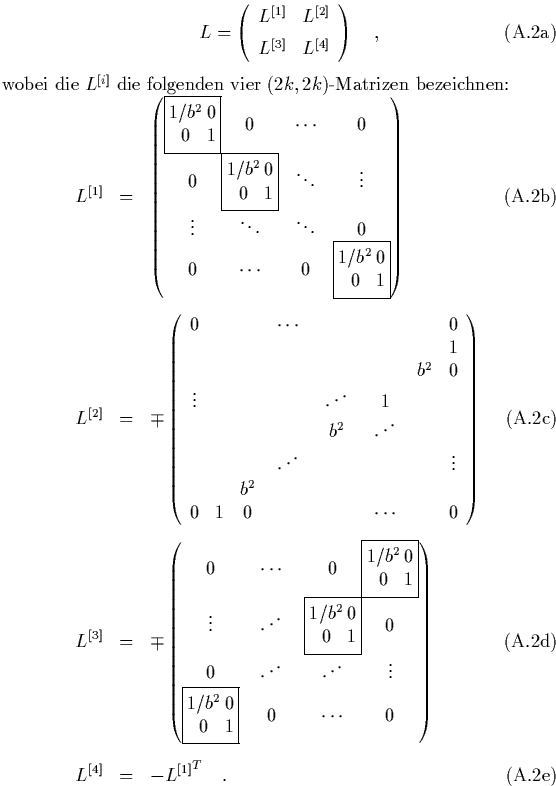
Formale Integrale für die Galinschen Normalformen:
 -Hamilton-Matrix:
-Hamilton-Matrix:
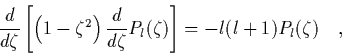 |
(A.-3) |
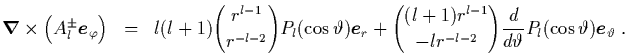 -Nullmatrizen mit dem Index
-Nullmatrizen mit dem Index
Offensichtlich ist die Jordan-Chevalley-Zerlegung von ![]() durch
durch
![]()
gegeben, so daß wir für das formale Integral der
Galin-Normalform I
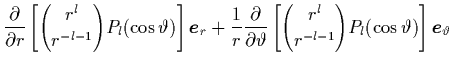 |
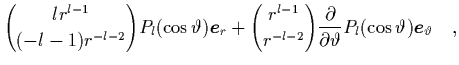 |
||
| (A.-3) |
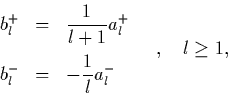 |
(A.-3) |
| (A.-2) |
| (A.-1) |
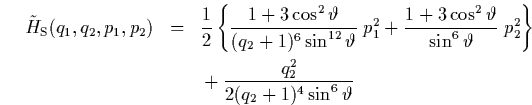 . Für
. Für | (A.-1) |
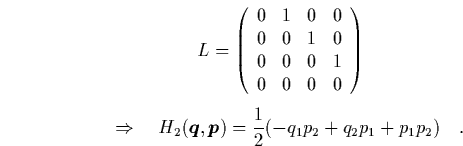 -Matrix
-Matrix
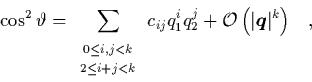 |
(A.0) |
| (A.1) |
| (A.2) |
Es ist uns bisher nicht gelungen, auch für ![]() das
DFS-Integral des Galinschen
das
DFS-Integral des Galinschen ![]() -Typs VI zu finden, weil
die Hamilton-Matrix hier schon recht kompliziert wird. Wir
erhalten für
-Typs VI zu finden, weil
die Hamilton-Matrix hier schon recht kompliziert wird. Wir
erhalten für ![]() :
:
![]()
Wir überlassen es dem Leser, die Jordan-Chevalley-Zerlegung
dieser ![]() -Hamilton-Matrix
-Hamilton-Matrix ![]() zu finden und damit
diejenigen Summanden von
zu finden und damit
diejenigen Summanden von ![]() zu identifizieren, die das
DFS-Integral im Fall VI konstituieren.
zu identifizieren, die das
DFS-Integral im Fall VI konstituieren.
Die Resultate des vorliegenden Anhanges A
lassen sich zu dem im folgenden dargestellten Verfahren zusammenzufassen,
nach dem ein Hamiltonsches System durch die Bestimmung eines zweiten
Integrals der Bewegung analysiert werden kann: