


Nächste Seite: Potenzreihenentwicklung der Størmer-Hamilton-Funktion
Aufwärts: arbeit
Vorherige Seite: Hamilton-Systeme beliebiger Dimension
Inhalt
Multipolentwicklung des magnetischen Vektorpotentials
In diesem Anhang zeigen wir, daß die Vektorpotentiale
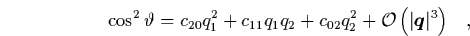
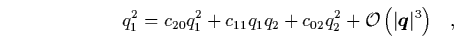
den skalaren Potentialen
![$\textstyle \parbox{11.5cm}{
\begin{displaymath}
\Phi_l^k(\rho,z) = \left\{ \b...
...;
\begin{array}{l} k=+ \\ [0.2cm] k=-
\end{array} \right.
\end{displaymath}}$](img1207.png)
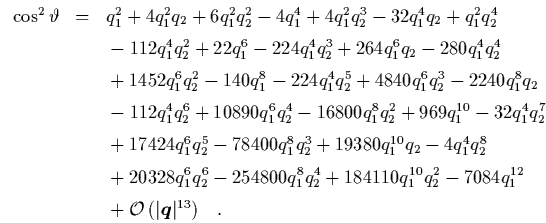
entsprechen, daß sie also für 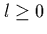 die Gleichung
die Gleichung
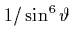
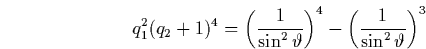
erfüllen.
Wir führen den Beweis zunächst für 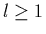 . Wir nutzen die Definition
der zugeordneten Legendre-Polynome,
. Wir nutzen die Definition
der zugeordneten Legendre-Polynome,
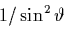 |
(B.1) |
aus und erhalten die Rotation von
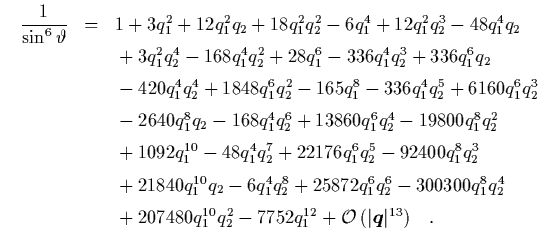 in
Kugelkoordinaten als
in
Kugelkoordinaten als
Der erste Summand läßt sich mit Hilfe der Legendreschen
Differentialgleichung,
![\begin{displaymath}
\frac{d}{d\zeta} \left[ \left( 1-\zeta^2 \right) \frac{d}{d\zeta}
P_l(\zeta) \right] = -l(l+1)P_l(\zeta) \quad,
\end{displaymath}](img1214.png) |
(B.2) |
umformen:
Andererseits gilt
so daß 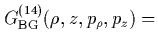 und
und 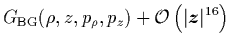 mit
mit
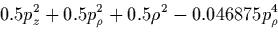 |
(B.3) |
der Gl. (2.12) genügen.
Es bleibt noch zu zeigen, daß diese Gleichung auch im Fall 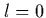 erfüllt wird. Für
erfüllt wird. Für 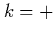 gilt:
gilt:
so daß wir 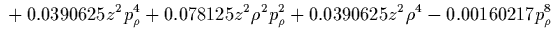 beliebig wählen können. Schließlich haben wir für
beliebig wählen können. Schließlich haben wir für
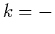 :
:
und 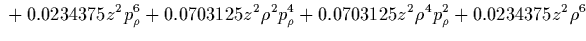 löst Gl. (2.12) mit
löst Gl. (2.12) mit
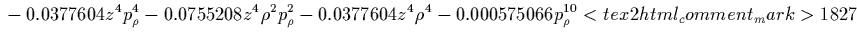 .
.



Nächste Seite: Potenzreihenentwicklung der Størmer-Hamilton-Funktion
Aufwärts: arbeit
Vorherige Seite: Hamilton-Systeme beliebiger Dimension
Inhalt
Martin_Engel
2000-05-25
![]()
![]()
![]()
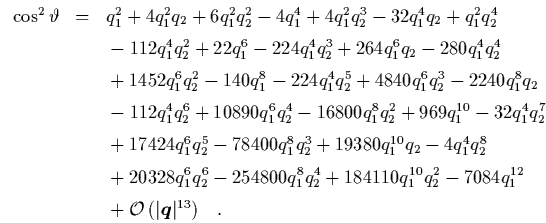
![]() die Gleichung
die Gleichung ![]()
![]()
![]() . Wir nutzen die Definition
der zugeordneten Legendre-Polynome,
. Wir nutzen die Definition
der zugeordneten Legendre-Polynome,
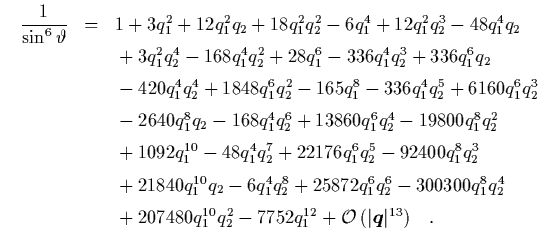 in
Kugelkoordinaten als
in
Kugelkoordinaten als
![\begin{displaymath}
\frac{d}{d\zeta} \left[ \left( 1-\zeta^2 \right) \frac{d}{d\zeta}
P_l(\zeta) \right] = -l(l+1)P_l(\zeta) \quad,
\end{displaymath}](img1214.png)

![$\displaystyle \frac{\partial}{\partial r} \left[ {r^l \choose r^{-l-1}}
P_l(\co...
...se r^{-l-1}} P_l(\cos\vartheta) \right]
{\mbox{\protect\boldmath$e$}}_\vartheta$](img1217.png)
![]() erfüllt wird. Für
erfüllt wird. Für ![]() gilt:
gilt: