


Nächste Seite: Die Normalform und das
Aufwärts: arbeit
Vorherige Seite: Multipolentwicklung des magnetischen Vektorpotentials
Inhalt
Potenzreihenentwicklung der Størmer-Hamilton-Funktion
Die in Dipolarkoordinaten formulierte Hamilton-Funktion des
Størmer-Problems kann so, wie sie in den Gln. (2.60) und (2.61) angegeben ist,
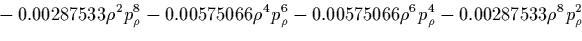 |
(C.1) |
(mit der durch Gl. (2.53) festgelegten Funktion
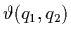 ),
noch nicht mit den Methoden der Normalformentheorie untersucht werden,
weil sie nicht als Potenzreihe vorliegt. Deswegen zeigen wir in diesem
Anhang, wie die zu den Gln. (2.60) und
(2.61) bzw. zu Gl. (C.1) gehörende
Potenzreihenentwicklung (2.62) in den Variablen
),
noch nicht mit den Methoden der Normalformentheorie untersucht werden,
weil sie nicht als Potenzreihe vorliegt. Deswegen zeigen wir in diesem
Anhang, wie die zu den Gln. (2.60) und
(2.61) bzw. zu Gl. (C.1) gehörende
Potenzreihenentwicklung (2.62) in den Variablen 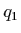 ,
,
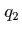 ,
, 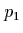 und
und 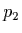 berechnet werden kann.
Wir orientieren uns dabei an der in [CoVl75] gegebenen
Darstellung, wo die Entwicklung allerdings nur bis zur sechsten
Ordnung durchgeführt wird. Dagegen gehen wir hier
bis zur zwölften Ordnung.
berechnet werden kann.
Wir orientieren uns dabei an der in [CoVl75] gegebenen
Darstellung, wo die Entwicklung allerdings nur bis zur sechsten
Ordnung durchgeführt wird. Dagegen gehen wir hier
bis zur zwölften Ordnung.
Zunächst suchen wir einen Ausdruck für
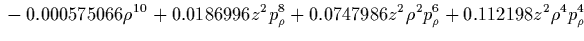 als Funktion
von
als Funktion
von 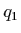 und
und 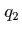 .
Durch Kombination von
(2.53a) und (2.53b) erhalten wir
.
Durch Kombination von
(2.53a) und (2.53b) erhalten wir
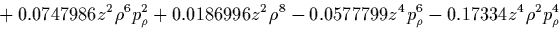 |
(C.2) |
eine implizite Gleichung für
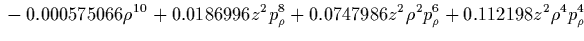 . Wir könnten sie
als Gleichung vierten Grades in
. Wir könnten sie
als Gleichung vierten Grades in
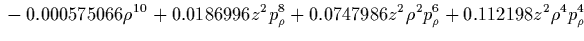 ansehen und mit Hilfe
der bekannten allgemeinen Lösungsformeln (vgl. [BrSe85, S. 133])
nach
ansehen und mit Hilfe
der bekannten allgemeinen Lösungsformeln (vgl. [BrSe85, S. 133])
nach
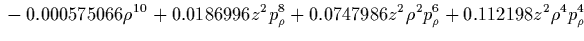 auflösen. Eine solche Lösung läge aber nicht in
Gestalt eines Polynoms in
auflösen. Eine solche Lösung läge aber nicht in
Gestalt eines Polynoms in 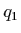 und
und 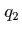 vor -- denn sie
enthielte zum Beispiel Wurzelausdrücke -- was im Hinblick auf die
Potenzreihenentwicklung von Gl. (C.1)
nachteilig wäre: Die auftretenden Wurzeln müßten ihrerseits
entwickelt werden.
Deswegen werden wir Gl. (C.2) von vornherein
näherungsweise lösen. Dazu setzen wir an:
vor -- denn sie
enthielte zum Beispiel Wurzelausdrücke -- was im Hinblick auf die
Potenzreihenentwicklung von Gl. (C.1)
nachteilig wäre: Die auftretenden Wurzeln müßten ihrerseits
entwickelt werden.
Deswegen werden wir Gl. (C.2) von vornherein
näherungsweise lösen. Dazu setzen wir an:
wobei das Symbol
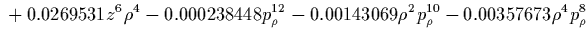 wieder andeuten soll, daß wir alle Summanden
wieder andeuten soll, daß wir alle Summanden
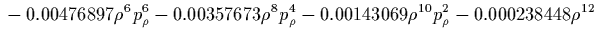 mit einem Totalgrad
mit einem Totalgrad 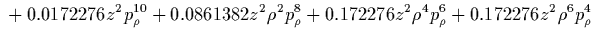 vernachlässigen.
Diesen Ansatz setzen wir in Gl. (C.2) ein und bestimmen
die
vernachlässigen.
Diesen Ansatz setzen wir in Gl. (C.2) ein und bestimmen
die 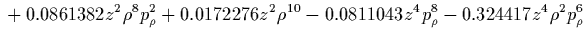 durch Koeffizientenvergleich.
Für
durch Koeffizientenvergleich.
Für 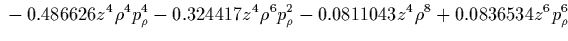 haben wir
haben wir
und Gl. (C.2) ergibt damit
so daß wir gefunden haben, daß in niedrigster Ordnung
gilt. Wie man sieht, zieht diese Vorgehensweise eine vergleichsweise
triviale, aber langwierige und fehleranfällige Arbeit nach sich,
so daß wir es vorgezogen haben, sie mit Hilfe von MATHEMATICA
[Wo91], einem Programm zur symbolischen Manipulation
mathematischer Ausdrücke, auszuführen. Das Ergebnis der Entwicklung
bis zur zwölften Ordnung einschließlich ist
 |
(C.3) |
Analog zur obenstehenden Vorgehensweise berechnen wir ebenfalls eine
Näherung
für
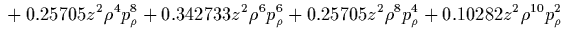 , indem wir zunächst aus den Gln. (2.53a) und (2.53b)
, indem wir zunächst aus den Gln. (2.53a) und (2.53b)
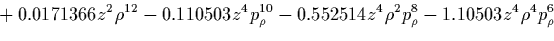 |
(C.4) |
folgern, wieder durch Koeffizientenvergleich nach
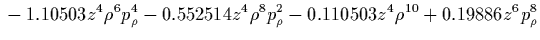 auflösen und dieses schließlich zur
dritten Potenz erheben. Das Resultat ist:
auflösen und dieses schließlich zur
dritten Potenz erheben. Das Resultat ist:
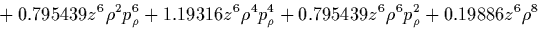 |
(C.5) |
Schließlich gilt nach dem verallgemeinerten binomischen Satz für
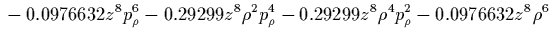 und
und 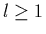 :
:
Nun können wir die einzelnen Bestimmungsstücke gemäß Gl. (C.1) ausmultiplizieren und
erhalten die gesuchte Potenzreihenentwicklung der Størmerschen Hamilton-Funktion:
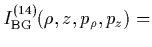
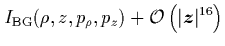



Nächste Seite: Die Normalform und das
Aufwärts: arbeit
Vorherige Seite: Multipolentwicklung des magnetischen Vektorpotentials
Inhalt
Martin_Engel
2000-05-25
![]() als Funktion
von
als Funktion
von ![]() und
und ![]() .
Durch Kombination von
(2.53a) und (2.53b) erhalten wir
.
Durch Kombination von
(2.53a) und (2.53b) erhalten wir
![]() , indem wir zunächst aus den Gln. (2.53a) und (2.53b)
, indem wir zunächst aus den Gln. (2.53a) und (2.53b)
![]() und
und ![]() :
:
![]()
![]()