Besides the coherent states there exist other, more general types of
states with minimum uncertainty product (A.45). Among
these, the coherent states are distinguished by having the same
uncertainties
with respect to the position and momentum operators for
![]() , as expressed by equation (A.46). Therefore
it seems reasonable to consider a broader class of states that satisfy
equation (A.45) but not equation
(A.46). These squeezed states
[Ken27,Yue76,HG88]
facilitate a very
compact
definition of the HUSIMI distribution
function in
subsection A.3.3 below.
The following exposition of the subject does not begin with a discussion
of standard deviations, but is organized
on the analogy of
subsection A.3.1.
The above observations concerning
, as expressed by equation (A.46). Therefore
it seems reasonable to consider a broader class of states that satisfy
equation (A.45) but not equation
(A.46). These squeezed states
[Ken27,Yue76,HG88]
facilitate a very
compact
definition of the HUSIMI distribution
function in
subsection A.3.3 below.
The following exposition of the subject does not begin with a discussion
of standard deviations, but is organized
on the analogy of
subsection A.3.1.
The above observations concerning
![]() and
and
![]() can then be
concluded from the definitions.
can then be
concluded from the definitions.
In subsection A.3.1 the coherent states have been introduced
as the eigenstates of the annihilation operator ![]() . The essential steps
of that definition can
be followed just as well
with respect to the
generalized annihilation operator
. The essential steps
of that definition can
be followed just as well
with respect to the
generalized annihilation operator
![[*]](crossref.png) .
.
Again, an explicit formula for
![]() may be found
by expanding it with respect to the eigenstates
may be found
by expanding it with respect to the eigenstates
![]() of the harmonic oscillator. From the ansatz
of the harmonic oscillator. From the ansatz
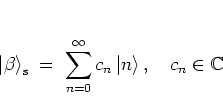 |
(A.40) |
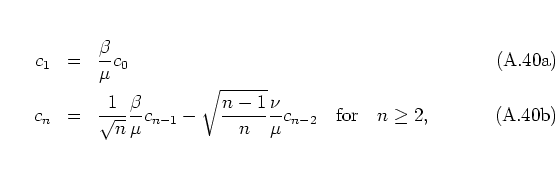
If ![]() ,
, ![]() satisfy
satisfy ![]() then
then
![]() can be normalized:
For any
can be normalized:
For any ![]() one can choose constants
one can choose constants
![]() and
and
![]() such
that for
such
that for ![]() it follows from
it follows from
![]() that
that
![]() .
For
.
For ![]() one can then show by induction and application of the
majorant criterion that the series
one can then show by induction and application of the
majorant criterion that the series
![]() converges, thus giving the finite
norm of
converges, thus giving the finite
norm of
![]() .
In the following,
.
In the following, ![]() is always chosen in such a way that
is always chosen in such a way that
![]() is normalized.
As an interim result, analogous to the findings concerning
is normalized.
As an interim result, analogous to the findings concerning
![]() in the previous subsection, one notes that every
in the previous subsection, one notes that every
![]() is an eigenvalue of
is an eigenvalue of ![]() , as long as
, as long as ![]() holds.
holds.
For the above considerations any values ![]() and
and ![]() satisfying
satisfying
![]() can be chosen.
Moreover,
the
recurrence
relation
(A.57) shows that
can be chosen.
Moreover,
the
recurrence
relation
(A.57) shows that
![]() depends on the
quotients
depends on the
quotients
![]() and
and ![]() only, such that
without loss of generality
either
only, such that
without loss of generality
either
![]() or
or ![]() can be chosen
without any further restriction.
In order to achieve as close an analogy between the operators
can be chosen
without any further restriction.
In order to achieve as close an analogy between the operators ![]() and
and
![]() as possible, I require
as possible, I require ![]() and
and ![]() to satisfy
to satisfy
![\begin{displaymath}[\b,\b^\dagger]\; = \; [{\hat{a}},{\hat{a}}^\dagger] \; = \; 1;
\end{displaymath}](img1415.png) |
(A.41) |
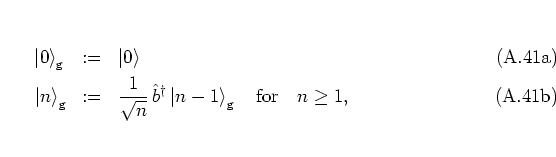
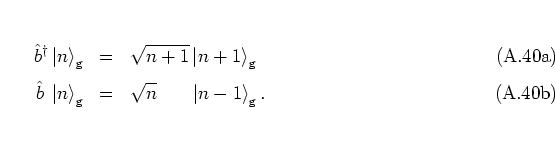
Using
the eigenvalue equation (A.55) and
the ![]() -representation of
-representation of ![]() and
and ![]() that can be derived from
equations (A.24) and (A.54),
that can be derived from
equations (A.24) and (A.54),
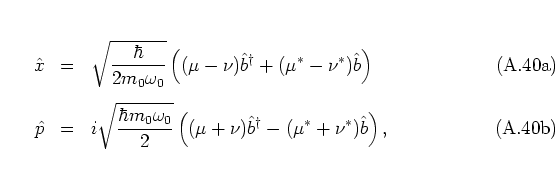
the uncertainties of
the position and momentum operators for the squeezed state
![]() are obtained as
are obtained as
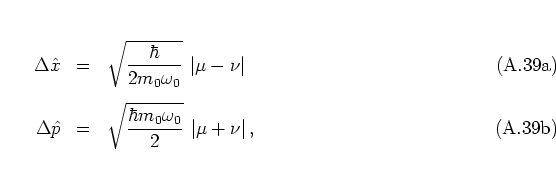
thus giving
the uncertainty product
The use of the term squeezed states for the eigenstates
![]() of
of ![]() ,
including those with uncertainty product larger than
,
including those with uncertainty product larger than
![]() ,
is motivated by the comparison of equation (A.64) with
the
uncertainties
(A.44c, A.44d)
of the coherent states
,
is motivated by the comparison of equation (A.64) with
the
uncertainties
(A.44c, A.44d)
of the coherent states
![]() : depending on
: depending on ![]() and
and ![]() , the
, the
![]() ,
,
![]() for
for
![]() can be made smaller
than those for
can be made smaller
than those for
![]() ; in other words, the former
can be
``squeezed'' [KS95].
In addition, in general
; in other words, the former
can be
``squeezed'' [KS95].
In addition, in general
![]() and
and
![]() are not
equal
even if
are not
equal
even if ![]() ; this is also contrasted by the coherent
states for which equation (A.46) holds, expressing just
this equality.
More on squeezing -- with respect to the HUSIMI distribution --
can be found in section A.6.
; this is also contrasted by the coherent
states for which equation (A.46) holds, expressing just
this equality.
More on squeezing -- with respect to the HUSIMI distribution --
can be found in section A.6.
For the time evolution of the squeezed states with respect to the
harmonic oscillator
Hamiltonian (A.47) one has -- in close analogy to
equation (A.48) --
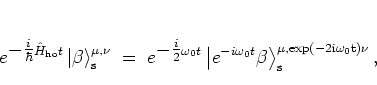 |
(A.40) |
In the literature (e.g. in [HG88,Lee95]), the most
frequently studied special case of squeezed states is that one that
finally leads to the definition of the HUSIMI distribution function.
The starting point for this discussion is the attempt to rewrite the
generalized annihilation operator
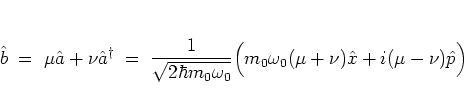 |
(A.41) |