

Next: The Complementary Case: Nonresonance
Up: The Stochastic Web
Previous: The Influence of the
Contents
Diffusive Energy Growth in the Channels
The time evolution of the stochastic web shown in figure 1.7
allows the conclusion that with a growing number of iterations of the web
map
an increasingly large
region of phase space is covered by orbit points.
This observation can be cast into a more exact form by considering the
energy
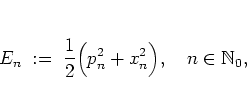 |
(1.46) |
for a particle moving within the stochastic web.
Obviously, 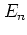 is the well-defined energy only between
the kicks, namely between the
is the well-defined energy only between
the kicks, namely between the 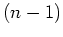 -st and the
-st and the 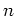 -th kick.
-th kick.
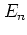 grows
quadratically
with the distance of the
particle from the origin of the phase plane.
grows
quadratically
with the distance of the
particle from the origin of the phase plane.
Figure 1.16
Figure 1.16:
The energy 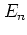 of the kicked harmonic oscillator for
of the kicked harmonic oscillator for 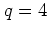 (
(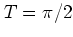 )
versus the number
)
versus the number 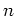 of kicks.
(a)
of kicks.
(a) 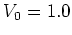 ; (b)
; (b) 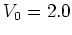 .
The initial values are
.
The initial values are 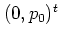 with the values of
with the values of
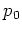 given in the insets.
given in the insets.
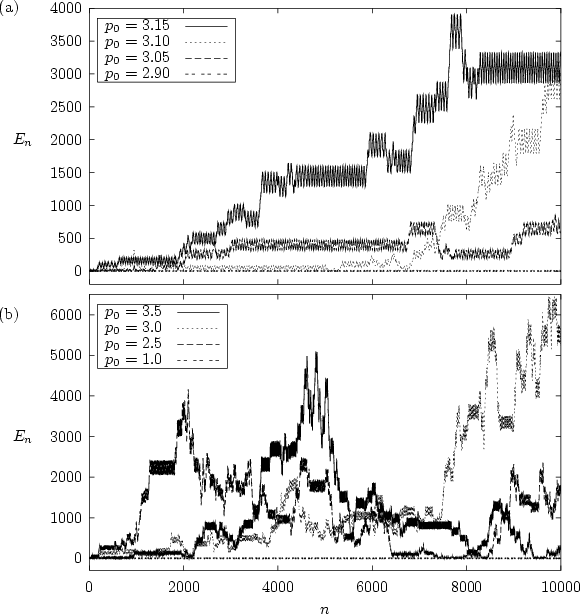 |
shows how, for 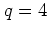 , the energy develops as a function
of time for some typical orbits and for two different values of
, the energy develops as a function
of time for some typical orbits and for two different values of 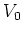 .
Two entirely different types of motion can be distinguished:
first,
if the initial condition
.
Two entirely different types of motion can be distinguished:
first,
if the initial condition 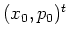 of the orbit is
chosen from one of the regular regions where invariant
lines
persist,
then
of the orbit is
chosen from one of the regular regions where invariant
lines
persist,
then 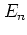 remains bounded as the orbit revolves on its
corresponding invariant
line.
The orbits with
remains bounded as the orbit revolves on its
corresponding invariant
line.
The orbits with 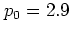 in figure
1.16a and
in figure
1.16a and 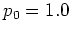 in figure 1.16b
are of this type,
giving rise to the nearly horizontal lines at
in figure 1.16b
are of this type,
giving rise to the nearly horizontal lines at 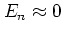 .
Second, for initial conditions within the channels of the web, unbounded
motion is possible and dominates the dynamics. The other orbits in
figure 1.16 correspond to initial conditions of this
class. This type of motion
manifests itself by sharp
increases and declines
in the energy. Between the
times of
rapidly changing
energy there are time
intervals for which the energy
remains roughly constant.
The length of
these time intervals varies and typically decreases with increasing values
of
.
Second, for initial conditions within the channels of the web, unbounded
motion is possible and dominates the dynamics. The other orbits in
figure 1.16 correspond to initial conditions of this
class. This type of motion
manifests itself by sharp
increases and declines
in the energy. Between the
times of
rapidly changing
energy there are time
intervals for which the energy
remains roughly constant.
The length of
these time intervals varies and typically decreases with increasing values
of 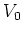 .
.
For orbits of the second type, on the average the energy grows with time;
this is the most prominent feature of the dynamics in the channels of
the web.
For computational convenience this time average can be
replaced by an ensemble average. Rather than considering a very long
orbit for a single initial condition I generate a
family of orbits,
corresponding to a
Gaussian
distribution of initial values, and compute
the accordingly averaged energy
at
time 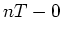 ,
,
denoted by
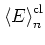 .1.10Using an ensemble average also allows for a more straightforward
comparison with the quantum dynamics of the system, since in quantum
mechanics HEISENBERG's uncertainty relation rules out the
possibility of considering
.1.10Using an ensemble average also allows for a more straightforward
comparison with the quantum dynamics of the system, since in quantum
mechanics HEISENBERG's uncertainty relation rules out the
possibility of considering 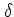 -shaped initial distributions
(corresponding to single classical initial values)
in phase space.
-shaped initial distributions
(corresponding to single classical initial values)
in phase space.
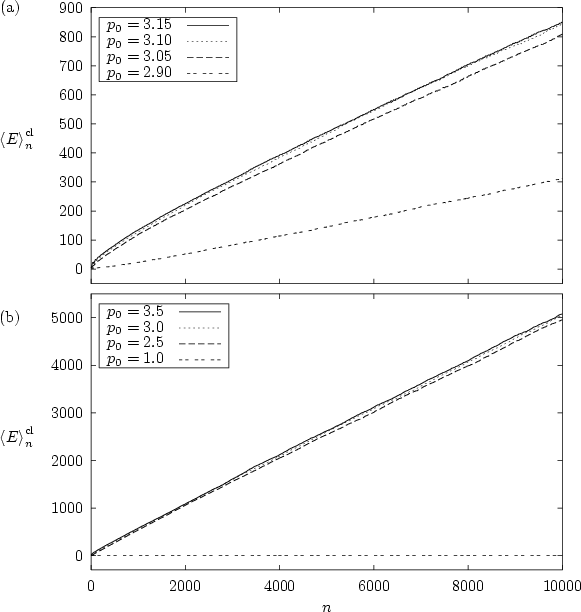
In figure 1.17
Figure 1.17:
The averaged energy
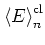 of the kicked harmonic
oscillator for
of the kicked harmonic
oscillator for 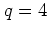 (
(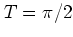 )
versus the number
)
versus the number 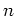 of kicks.
(a)
of kicks.
(a) 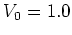 ; (b)
; (b) 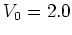 .
For each graph
.
For each graph  initial values are used which are
distributed according to a
Gaussian
with half width 0.1,
centered around the same initial values as in figure
1.16.
initial values are used which are
distributed according to a
Gaussian
with half width 0.1,
centered around the same initial values as in figure
1.16.
 |
I employ
Gaussian
distributions of initial conditions which are
centred around the initial conditions of the preceding figure. The
Gaussians
used here are of half width 0.1, both in 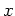 - and
- and
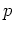 -direction.
From these curves it is quite clear that the gross
oscillations seen in figure 1.16 cancel as a result
of the averaging over many orbits. Initial distributions centred in
regular regions of phase space yield a slower increase of the energy at
first, but
due to the tails of the Gaussian distributions
even in these cases the averaged energy is not bounded any more.
-direction.
From these curves it is quite clear that the gross
oscillations seen in figure 1.16 cancel as a result
of the averaging over many orbits. Initial distributions centred in
regular regions of phase space yield a slower increase of the energy at
first, but
due to the tails of the Gaussian distributions
even in these cases the averaged energy is not bounded any more.
After averaging it becomes obvious that -- apart from a brief
(
![$n {\protect\begin{array}{c}
<\protect\\ [-0.3cm]\sim
\protect\end{array}} 1000$](img332.png) )
transient
stage of subdiffusive motion -- the growth of the energy
is characterized by normal or EINSTEIN diffusion
[Ein06],
i.e. the averaged energy
grows as a
)
transient
stage of subdiffusive motion -- the growth of the energy
is characterized by normal or EINSTEIN diffusion
[Ein06],
i.e. the averaged energy
grows as a
linear function of time,
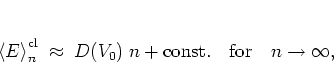 |
(1.47) |
with a
diffusion coefficient 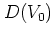 .
As indicated by the above figures,
.
As indicated by the above figures, 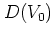 should be expected to be a function of the amplitude
should be expected to be a function of the amplitude 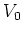 of the kicks,
but independent of
of the kicks,
but independent of 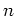 .
.
For larger values of 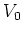 a formula for
a formula for 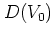 can be derived
analytically, which holds (with deviations which are discussed
below) for all web maps with
can be derived
analytically, which holds (with deviations which are discussed
below) for all web maps with
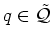 . From
equation (1.21) it follows that
for a single orbit
the energy change inflicted by the
. From
equation (1.21) it follows that
for a single orbit
the energy change inflicted by the
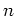 -th kick is determined by
-th kick is determined by
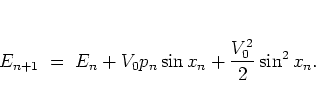 |
(1.48) |
Averaging over 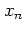 and
and 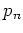 then gives
then gives
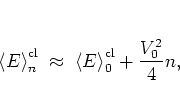 |
(1.49) |
such that I have for the diffusion coefficient:
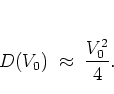 |
(1.50) |
This derivation, which is
largely analogous to the
random phase approximation for the kicked rotor
[Chi79,CCIF79]
(see also subsection 5.1.1),
relies on the
straightforward
averaging over 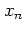 and
and
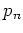 .
Roughly, it can be taken to be
justified if unbounded
and unhindered
motion into all directions of the phase plane is
possible, i.e. if
.
Roughly, it can be taken to be
justified if unbounded
and unhindered
motion into all directions of the phase plane is
possible, i.e. if
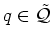 ,
and if, in addition, the channels are wide enough, i.e. if
,
and if, in addition, the channels are wide enough, i.e. if 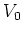 is large
enough.
For aperiodic webs, on the other hand, the dynamics is
subdiffusive,
because the nonperiodicity implies that in general the channels of the webs
are not wide enough everywhere for unrestricted diffusion through all the
channels (cf. [Hip94]).
is large
enough.
For aperiodic webs, on the other hand, the dynamics is
subdiffusive,
because the nonperiodicity implies that in general the channels of the webs
are not wide enough everywhere for unrestricted diffusion through all the
channels (cf. [Hip94]).
The quality of the
approximation leading
to equation
(1.78)
is checked in figure 1.18
for the case of 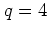 .
.
For several values of 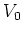 I have calculated
I have calculated
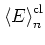 and
obtained
and
obtained 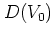 using a least squares fit;1.11these values of the diffusion coefficient are compared with the graph of
formula (1.78).
By and large, agreement of the two can be observed. But it is also a
striking feature of figure 1.18
that an additional oscillation of the diffusion coefficient
is found to be superimposed to the expected parabola.
Following [KM90]
such oscillations of the diffusion coefficient
can be attributed to
autocorrelations of the
orbits, due to small islands of stability in the channels of the web,
while strictly speaking the
(``quasilinear'')
result (1.78) holds for Markovian dynamics only
[CM81,Rei98].
For a more detailed analysis of the parameter dependence of the diffusion
coefficient
for the
kicked harmonic oscillator see
[DH95,DH97].
using a least squares fit;1.11these values of the diffusion coefficient are compared with the graph of
formula (1.78).
By and large, agreement of the two can be observed. But it is also a
striking feature of figure 1.18
that an additional oscillation of the diffusion coefficient
is found to be superimposed to the expected parabola.
Following [KM90]
such oscillations of the diffusion coefficient
can be attributed to
autocorrelations of the
orbits, due to small islands of stability in the channels of the web,
while strictly speaking the
(``quasilinear'')
result (1.78) holds for Markovian dynamics only
[CM81,Rei98].
For a more detailed analysis of the parameter dependence of the diffusion
coefficient
for the
kicked harmonic oscillator see
[DH95,DH97].
Footnotes
- ....1.10
-
The superscript
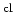 is used to distinguish the classical
ensemble average
is used to distinguish the classical
ensemble average
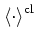 from the quantum
expectation value
from the quantum
expectation value
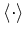 .
.
- ... fit;1.11
-
More sophisticated methods for
determining the speed of diffusion can be found in the literature; see
for example [Hip94] and references therein.



Next: The Complementary Case: Nonresonance
Up: The Stochastic Web
Previous: The Influence of the
Contents
Martin Engel 2004-01-01
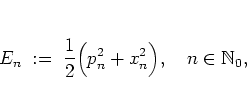

![]() ,
,
![]() .1.10Using an ensemble average also allows for a more straightforward
comparison with the quantum dynamics of the system, since in quantum
mechanics HEISENBERG's uncertainty relation rules out the
possibility of considering
.1.10Using an ensemble average also allows for a more straightforward
comparison with the quantum dynamics of the system, since in quantum
mechanics HEISENBERG's uncertainty relation rules out the
possibility of considering ![]() -shaped initial distributions
(corresponding to single classical initial values)
in phase space.
-shaped initial distributions
(corresponding to single classical initial values)
in phase space.

![$n {\protect\begin{array}{c}
<\protect\\ [-0.3cm]\sim
\protect\end{array}} 1000$](img332.png) )
transient
stage of subdiffusive motion -- the growth of the energy
is characterized by normal or EINSTEIN diffusion
[Ein06],
i.e. the averaged energy
grows as a
)
transient
stage of subdiffusive motion -- the growth of the energy
is characterized by normal or EINSTEIN diffusion
[Ein06],
i.e. the averaged energy
grows as a
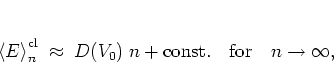
![]() a formula for
a formula for ![]() can be derived
analytically, which holds (with deviations which are discussed
below) for all web maps with
can be derived
analytically, which holds (with deviations which are discussed
below) for all web maps with
![]() . From
equation (1.21) it follows that
for a single orbit
the energy change inflicted by the
. From
equation (1.21) it follows that
for a single orbit
the energy change inflicted by the
![]() -th kick is determined by
-th kick is determined by
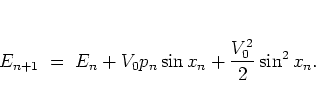
![]() .
.