Diffusing Wave Packets

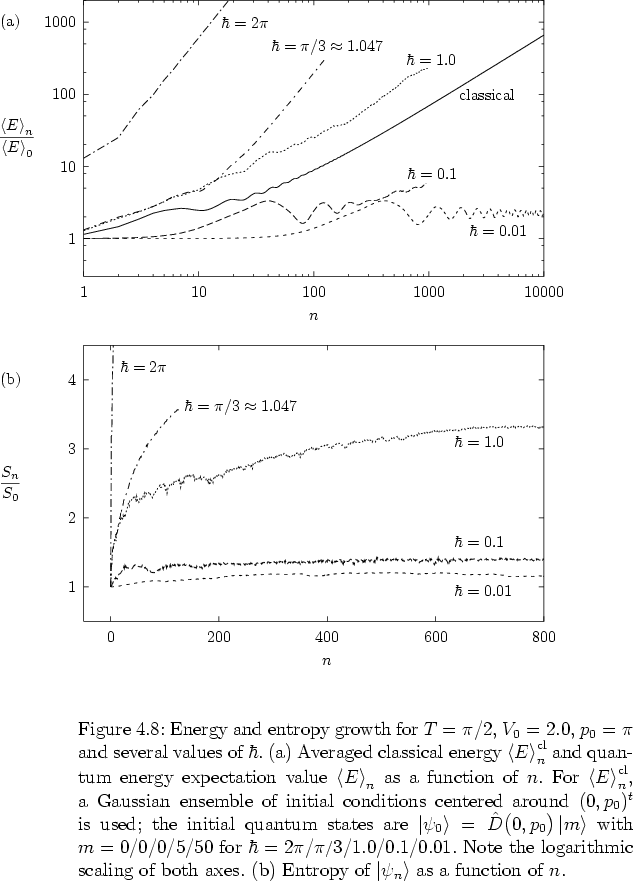
In subsection 1.2.4 I have discussed the diffusive energy growth in the channels of classical stochastic webs, i.e. in the cases of resonance given by equation (1.33). In the present subsection I study the quantum energy growth in these cases leading to the emergence of quantum stochastic webs, as shown in subsection 4.1.1 and in sections C.1 and C.2 of the appendix.

Figures 4.8a and 4.9a

display the quantum energy expectation value

$$\left< E \right>_n \; = \; \left< E \right>\Big\vert _{t=nT-... ...rt a_m^{(n)} \right\vert^2 \, \hbar\left(m+\frac{1}{2}\right)$$ (4.3)

as a function of discretized time for rectangular and hexagonal stochastic webs with $T=\pi /2$ and $T=2\pi /3$. The results of numerical simulations for several values of $\hbar$ are shown, where the initial states are located at the unstable periodic points $(0,\pi)^t$ and $(0,2\pi/\sqrt{3})^t$ of intersections of separatrices, as seems suitable for studying unbounded dynamics. The figures are for $V_0=2.0$ -- other values of $V_0$ lead to similar results; but note that very large values of $V_0{ {\protect\begin{array}{c} >\protect\\ [-0.3cm]\sim \protect\end{array}} }10.0$ can lead to a very fast spreading of the states and thus may necessitate to stop the algorithm after only a short period of time. For comparison, results for $\left< E \right>_n^{\rm cl}$, i.e. for the ensemble averaged classical energies (1.74), of classical computations with corresponding parameter values are also shown.

Within the accuracy of the computation, the figures indicate that for generic values of $\hbar$ -- here: for $\hbar=1.0/0.1$; nongenericity of $\hbar$ in the present context is defined in equations (4.7) below -- the quantum energy grows in the same way as the classical energy average does: in the doubly logarithmic plots, the slopes of the respective graphs indicate an asymptotically linear dependence on time,

$$\left< E \right>_n \; \sim \; n.$$ (4.4)

Needless to say, this observation can only be made with respect to the scaling region of these graphs, i.e. for large enough $n$, after the initial transient dynamics has been left behind. For $\left< E \right>_n^{\rm cl}$ and $\hbar =1.0$ this is easily seen in the plots; for $\hbar =0.1$ the dynamics develops into linear energy growth just around the time when the simulation has to be terminated for numerical reasons; and for $\hbar =0.01$ the scaling region is not yet reached after even $10^4$ kicks. It would be desirable to further confirm the result of linear scaling by using a much larger $m_{\mbox{\scriptsize max}}$. But this requires some considerable additional numerical effort, and no other result than linear energy growth should be expected to be found for these generic values of $\hbar$.

Many more results of this kind, for other values of generic $\hbar$ and $V_0$, have been obtained numerically, but are not shown here. Similarly, numerical results with respect to the third nontrivial type of resonance, given by $T=\pi /3$, are not shown here either, but have been obtained in large numbers; they lead to similar observations as described above. Summarizing I have the result that, generically, in quantum mechanics diffusive energy growth within stochastic webs is obtained, just as in the classical case.

The figures also show results for some nongeneric values of $\hbar$. In the present context, $\hbar$ is called nongeneric if there is an integer $s$ such that

This definition of nongenericity of $\hbar$ is based on equations (4.44) and (4.49) below, which are obtained in a natural way in subsection 4.2.2 when analytically discussing dynamical consequences of the symmetries of quantum stochastic webs. The cases of nongeneric $\hbar$ as given by equations (4.7) are examples of quantum resonances; this is explained in subsection 4.2.2 as well.

With more than convincing numerical accuracy, the figures -- with $s=1$ and $s=6$ in figure 4.8, and $s=1$ and $s=7$ in figure 4.9 -- indicate that these nongeneric values of $\hbar$ asymptotically lead to faster, namely quadratic, energy growth,

$$\left< E \right>_n \; \sim \; n^2,$$ (4.4)

as opposed to the linear $n$-dependence for generic $\hbar$-values. This ballistic energy growth result is remarkable, as for example the values of $\hbar =1.0$ and $\hbar=\pi/3\approx 1.047$ differ by less than five percent and still account for the much differing energy growth laws (4.6) and (4.8). Interestingly, for $n{ {\protect\begin{array}{c} <\protect\\ [-0.3cm]\sim \protect\end{array}} }10$ the curves for $\hbar =1.0$ and $\hbar=\pi/3$ agree within the numerical accuracy, due to the nearly identical values of $\hbar$. Only at later times the respective regimes of linear and quadratic energy growth take over, causing the slopes of the curves to take on differing values. The same observation holds for $\hbar =1.0$ and $\hbar=4\pi/7\sqrt{3}\approx 1.036$ in the case of $T=2\pi /3$.

Both energy growth rate results, diffusive (4.6) and ballistic (4.8), are given a theoretical explanation in section 4.2. Note that, irrespective of the (non-) genericity of the value of $\hbar$, for a given resonant $T$ always the same symmetric phase space patterns are obtained. In other words, depending on the value of $\hbar$, the same quantum stochastic web may be subject to diffusive or ballistic energy growth of the quantum state moving within the web.

Considering the diffusive energy growth of the quantum states $\left\vert \psi_n \right>$ is one way of discussing the spreading of the states in the phase plane with time. Another way is to discuss their VON NEUMANN entropy

$$S_n \; = \; S(nT-0) \; = \; -\sum_{m=0}^\infty \, \left\ve... ...^{(n)} \right\vert^2 \log \left\vert a_m^{(n)} \right\vert^2.$$ (4.5)

According to [MS99], $S_n$ can be related to the classical KOLMOGOROV-SINAI entropy [BS93], and it can be interpreted as a measure for the degree to which the quantum state is spread within phase space. With this interpretation of $S_n$, but without going deeper into the theory of quantum entropies, figures 4.8b and 4.9b, showing $S_n$ as a function of time, indicate that the corresponding sequences of quantum states continuously cover larger and larger portions of phase space -- in agreement with the result obtained with respect to the energies of these dynamics.