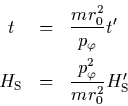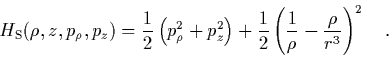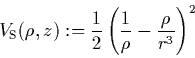


Nächste Seite: Diskussion des Størmer-Potentials
Aufwärts: Das Størmer-Problem
Vorherige Seite: Das Størmer-Problem
Inhalt
Bestimmung der Hamilton-Funktion
Für die Beschreibung des zu dem Dipolmoment
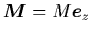 gehörenden Dipolmagnetfeldes
gehörenden Dipolmagnetfeldes
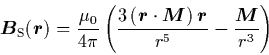 |
(2.42) |
haben wir im Rahmen der Multipolentwicklung von Abschnitt
2.1 offensichtlich zu wählen:
wie man aus Tabelle 2.2 entnehmen kann.
Eine Formel
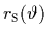 für die Feldlinien des Størmer-Magnetfeldes
für die Feldlinien des Størmer-Magnetfeldes
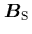 berechnet man am einfachsten in Kugelkoordinaten.
Wir schreiben das Magnetfeld als
berechnet man am einfachsten in Kugelkoordinaten.
Wir schreiben das Magnetfeld als
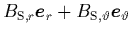 und
schließen aus Gl. (2.26)
und
schließen aus Gl. (2.26)
Die allgemeine Lösung dieser Differentialgleichung erhalten wir als
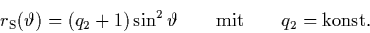 |
(2.44) |
Der Grund für die
ungewöhnliche Schreibweise des konstanten Vorfaktors als 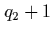 wird im Zusammenhang mit den
in Abschnitt 2.4.3
einzuführenden
Dipolarkoordinaten klar werden.
In Abbildung 2.4
sind die wohlbekannten Størmer-Magnetfeldlinien der Gl. (2.44) dargestellt.
wird im Zusammenhang mit den
in Abschnitt 2.4.3
einzuführenden
Dipolarkoordinaten klar werden.
In Abbildung 2.4
sind die wohlbekannten Størmer-Magnetfeldlinien der Gl. (2.44) dargestellt.
Mit dem zu
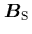 gehörenden Vektorpotential
gehörenden Vektorpotential
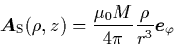 |
(2.45) |
erhält man aus Gl. (2.16) die entsprechende
Størmer-Hamilton-Funktion als
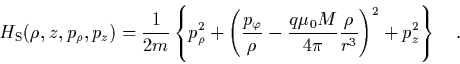 |
(2.46) |
Durch eine geeignete Skalierung vereinfachen wir diese Hamilton-Funktion,
wobei wir einen etwas anderen Weg als in [Se90] beschreiten. Dort
wurden die Ortsraumkoordinaten mit der sogenannten
Størmer-Einheit
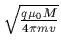 (mit
(mit
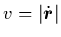 ) skaliert, was letztlich auf
eine Hamilton-Funktion führt, die die Bewegung bei der konstanten Energie
) skaliert, was letztlich auf
eine Hamilton-Funktion führt, die die Bewegung bei der konstanten Energie
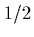 beschreibt.
beschreibt. 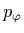 verbleibt als ein frei wählbarer Parameter
des Systems.
Hingegen ziehen wir hier -- im Einklang mit [DrFi79] und
analog zu den anderen oben betrachteten Modellsystemen -- eine Skalierung
vor, die
auf eine Hamilton-Funktion führt, die nicht mehr parameterabhängig ist
und statt dessen einem System mit einer nicht-konstanten, frei wählbaren
Energie entspricht. Dazu skalieren wir wie in [CoVl75]
Längen mit
verbleibt als ein frei wählbarer Parameter
des Systems.
Hingegen ziehen wir hier -- im Einklang mit [DrFi79] und
analog zu den anderen oben betrachteten Modellsystemen -- eine Skalierung
vor, die
auf eine Hamilton-Funktion führt, die nicht mehr parameterabhängig ist
und statt dessen einem System mit einer nicht-konstanten, frei wählbaren
Energie entspricht. Dazu skalieren wir wie in [CoVl75]
Längen mit
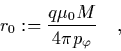 |
(2.47) |
das heißt, wir führen gestrichene Größen ein, indem wir
![\begin{displaymath}
\begin{array}{rcl}
\rho & = & r_0 \rho' \\ [0.2cm]
z & = & r_0 z'
\end{array}\end{displaymath}](img659.png) |
(2.48) |
setzen und außerdem
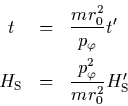 |
(2.49) |
benutzen,
so daß wir schließlich zu der folgenden skalierten
Hamilton-Funktion für
das Størmer-Problem gelangen (die Strichmarkierungen werden wieder der
Einfachheit halber weggelassen):
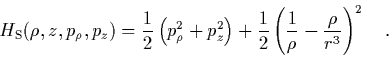 |
(2.50) |
Man kann diese Funktion auffassen als die Hamilton-Funktion eines
Teilchens mit zwei Freiheitsgraden der Bewegung, das sich im
,,Størmer-Potential``
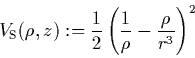 |
(2.51) |
bewegt.



Nächste Seite: Diskussion des Størmer-Potentials
Aufwärts: Das Størmer-Problem
Vorherige Seite: Das Størmer-Problem
Inhalt
Martin_Engel
2000-05-25
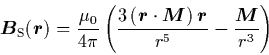
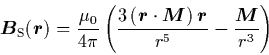
![]() für die Feldlinien des Størmer-Magnetfeldes
für die Feldlinien des Størmer-Magnetfeldes
![]() berechnet man am einfachsten in Kugelkoordinaten.
Wir schreiben das Magnetfeld als
berechnet man am einfachsten in Kugelkoordinaten.
Wir schreiben das Magnetfeld als
![]() und
schließen aus Gl. (2.26)
und
schließen aus Gl. (2.26)
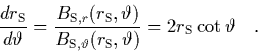
![]() gehörenden Vektorpotential
gehörenden Vektorpotential
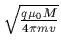 (mit
(mit
![]() ) skaliert, was letztlich auf
eine Hamilton-Funktion führt, die die Bewegung bei der konstanten Energie
) skaliert, was letztlich auf
eine Hamilton-Funktion führt, die die Bewegung bei der konstanten Energie
![]() beschreibt.
beschreibt. ![]() verbleibt als ein frei wählbarer Parameter
des Systems.
Hingegen ziehen wir hier -- im Einklang mit [DrFi79] und
analog zu den anderen oben betrachteten Modellsystemen -- eine Skalierung
vor, die
auf eine Hamilton-Funktion führt, die nicht mehr parameterabhängig ist
und statt dessen einem System mit einer nicht-konstanten, frei wählbaren
Energie entspricht. Dazu skalieren wir wie in [CoVl75]
Längen mit
verbleibt als ein frei wählbarer Parameter
des Systems.
Hingegen ziehen wir hier -- im Einklang mit [DrFi79] und
analog zu den anderen oben betrachteten Modellsystemen -- eine Skalierung
vor, die
auf eine Hamilton-Funktion führt, die nicht mehr parameterabhängig ist
und statt dessen einem System mit einer nicht-konstanten, frei wählbaren
Energie entspricht. Dazu skalieren wir wie in [CoVl75]
Längen mit
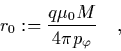
![\begin{displaymath}
\begin{array}{rcl}
\rho & = & r_0 \rho' \\ [0.2cm]
z & = & r_0 z'
\end{array}\end{displaymath}](img659.png)