Welche Eigenschaften des oben diskutierten Feldes
![]() sind nun
wesentlich für den Einschluß des Teilchens? Dies ist eine sinnvolle und
wichtige Frage, solange man nicht ein konkretes System beschreiben,
sondern ganz allgemein magnetische Flaschen und deren charakteristische
Eigenschaften diskutieren will. Wir suchen
also ein Magnetfeld,
das ebenso wie
sind nun
wesentlich für den Einschluß des Teilchens? Dies ist eine sinnvolle und
wichtige Frage, solange man nicht ein konkretes System beschreiben,
sondern ganz allgemein magnetische Flaschen und deren charakteristische
Eigenschaften diskutieren will. Wir suchen
also ein Magnetfeld,
das ebenso wie
![]() zu einer gebundenen Bewegung des
Teilchens
führt, dabei aber ,,einfacher`` ist. Dies ist insbesondere für die
sich anschließende Berechnung der entsprechenden Normalform von
Bedeutung, denn der Vergleich einiger Normalformtransformationen in
Kapitel 5 wird zeigen, daß
die Normalform einer Hamilton-Funktion und ihr Quasiintegral um so
einfacher sind, je einfacher die Hamilton-Funktion selbst ist.
(In diesem Zusammenhang nennen
wir eine Hamilton-Funktion einfach, wenn sie aus nur wenigen Summanden
besteht.)
zu einer gebundenen Bewegung des
Teilchens
führt, dabei aber ,,einfacher`` ist. Dies ist insbesondere für die
sich anschließende Berechnung der entsprechenden Normalform von
Bedeutung, denn der Vergleich einiger Normalformtransformationen in
Kapitel 5 wird zeigen, daß
die Normalform einer Hamilton-Funktion und ihr Quasiintegral um so
einfacher sind, je einfacher die Hamilton-Funktion selbst ist.
(In diesem Zusammenhang nennen
wir eine Hamilton-Funktion einfach, wenn sie aus nur wenigen Summanden
besteht.)
Aus Abbildung 2.1 kann man entnehmen, daß die
einfachste Bewegung im Magnetfeld
![]() (im Falle
(im Falle
![]() ) in der Nähe einer
Feldlinie nahe der
) in der Nähe einer
Feldlinie nahe der ![]() -Achse stattfindet: Die Feldlinien verlaufen
dort fast parallel zur
-Achse stattfindet: Die Feldlinien verlaufen
dort fast parallel zur ![]() -Achse, mit lediglich einer
leichten Wölbung
in positiver
-Achse, mit lediglich einer
leichten Wölbung
in positiver
![]() -Richtung. Mittels ,,trial and error`` findet man
[DrFi79], daß das Magnetfeld
-Richtung. Mittels ,,trial and error`` findet man
[DrFi79], daß das Magnetfeld
![]() , welches
man aus (2.24) durch Fortlassen des Termes
, welches
man aus (2.24) durch Fortlassen des Termes
![]() erhält,
erhält,
Der offensichtliche Vorteil, ein -- zumindest formelmäßig --
einfacheres Magnetfeld zu erhalten, wird hier durch den Nachteil erkauft,
daß sich
![]() nicht in die in Abschnitt
2.1 diskutierte Multipolentwicklung einpaßt. Denn
laut Tabelle 2.2 ist
nicht in die in Abschnitt
2.1 diskutierte Multipolentwicklung einpaßt. Denn
laut Tabelle 2.2 ist
![]() der einzig mögliche
Grad-zwei-Anteil eines
der einzig mögliche
Grad-zwei-Anteil eines
![]() -Feldes, das dieser Entwicklung genügt.
Der Anteil von
-Feldes, das dieser Entwicklung genügt.
Der Anteil von
![]() vom Grad zwei ist aber per
Konstruktion von
vom Grad zwei ist aber per
Konstruktion von
![]() verschieden.
verschieden.
Ist
![]() demnach unphysikalisch und damit für uns irrelevant?
Nein, denn zunächst einmal besagt die Diskrepanz zwischen Gl. (2.34) und Tabelle 2.2
lediglich, daß die in Abschnitt 2.1 gemachten
Annahmen hier nicht zutreffen. So
läßt sich zum Beispiel das Postulat
der Stromfreiheit nicht mehr aufrechterhalten (wenn man weiterhin nur
stationäre Felder zulassen will), weil für das Dragt-Finn-Magnetfeld
aus der inhomogenen Maxwell-Gleichung
demnach unphysikalisch und damit für uns irrelevant?
Nein, denn zunächst einmal besagt die Diskrepanz zwischen Gl. (2.34) und Tabelle 2.2
lediglich, daß die in Abschnitt 2.1 gemachten
Annahmen hier nicht zutreffen. So
läßt sich zum Beispiel das Postulat
der Stromfreiheit nicht mehr aufrechterhalten (wenn man weiterhin nur
stationäre Felder zulassen will), weil für das Dragt-Finn-Magnetfeld
aus der inhomogenen Maxwell-Gleichung
![]() folgt:
folgt:
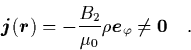 |
(2.36) |
Wir wollen jetzt die Hamilton-Funktion der Dragt-Finn-Magnetflasche
herleiten
und benötigen dafür ein Vektorpotential
![]() zu
zu
![]() . Um
. Um
| (2.37) |
| (2.38) |
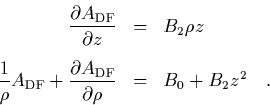
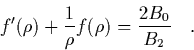
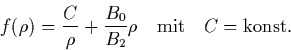
Wenn wir Gl. (2.39) in die allgemeine Formel
(2.16) für axialsymmetrische Magnetflaschen einsetzen
und wie bei der Brown-Gabrielse-Flasche ![]() annehmen,
ergibt sich für die Hamilton-Funktion der Dragt-Finn-Flasche:
annehmen,
ergibt sich für die Hamilton-Funktion der Dragt-Finn-Flasche:
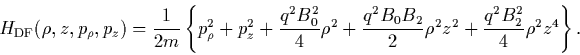 |
(2.40) |
Auch diese Hamilton-Funktion kann offensichtlich nicht mit den Mitteln Gustavsonschen Normalformentheorie behandelt werden.