In this subsection I discuss some of the problems of the theory developed in the previous subsections, and I outline how these problems can be either avoided or solved.
One of the issues that need to be addressed is to what degree quantum
localization can be expected when the matrix elements ![]() do not
decay rapidly enough with
do not
decay rapidly enough with ![]() .
This problem is not unique to the quantum kicked harmonic
oscillator;
the same can happen with respect to
the quantum kicked rotor:
figure 5.7 indicates that for larger
values of
.
This problem is not unique to the quantum kicked harmonic
oscillator;
the same can happen with respect to
the quantum kicked rotor:
figure 5.7 indicates that for larger
values of ![]() the quality of the tight binding approximation
deteriorates there, too.
In the literature, this is
obviously
not regarded as an obstacle to
ANDERSON localization in the kicked rotor, based on the tight binding
equation; at least, this problem is not addressed in the standard
literature.
But see [Kle97] for a discussion of this aspect, with a
positive result on localization in a particular ANDERSON model with
``long range hopping''.
the quality of the tight binding approximation
deteriorates there, too.
In the literature, this is
obviously
not regarded as an obstacle to
ANDERSON localization in the kicked rotor, based on the tight binding
equation; at least, this problem is not addressed in the standard
literature.
But see [Kle97] for a discussion of this aspect, with a
positive result on localization in a particular ANDERSON model with
``long range hopping''.
Judging from figures
5.18 and 5.19, such a
case of slow decay should be expected
in the quantum kicked harmonic oscillator
for larger values of ![]() and
and
![]() . Even in situations like this, localization is generically given.
This can be seen by replacing the tight binding equation
(5.101) with a similar approximation to
the discrete SCHRÖDINGER equation
(5.84), the only difference being that
now the interaction with neighbouring sites is assumed
to be characterized
by a suitably longer range
. Even in situations like this, localization is generically given.
This can be seen by replacing the tight binding equation
(5.101) with a similar approximation to
the discrete SCHRÖDINGER equation
(5.84), the only difference being that
now the interaction with neighbouring sites is assumed
to be characterized
by a suitably longer range ![]() (with even
(with even
![]() ):
):
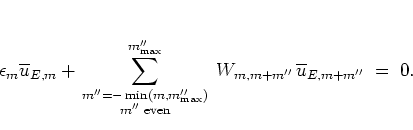 |
(5.91) |
The same technique helps to avoid the troubles that come with the
pathological cases where ![]() or
or ![]() for some
for some ![]() . The problem of
unavoidably having to divide by such a zero, as encountered in
subsections 5.3.2 and
5.3.3, simply vanishes for suitably
large
. The problem of
unavoidably having to divide by such a zero, as encountered in
subsections 5.3.2 and
5.3.3, simply vanishes for suitably
large ![]() if there
exists
nontrivial interaction between some
sites at all.
if there
exists
nontrivial interaction between some
sites at all.
The other, probably more satisfying, answer to the question of the
pathologically vanishing nearest neighbour interactions is the
following.
The matrix elements for nearest neighbour interaction can be regarded
as the values of a continuous function
![]() , sampled at
equidistant intervals on the
, sampled at
equidistant intervals on the ![]() -axis.
Figure 5.20 gives the impression that
-axis.
Figure 5.20 gives the impression that
![]() is well-behaved in the sense that all its intersections with the
is well-behaved in the sense that all its intersections with the
![]() -axis are transversal, and that the zeroes of
-axis are transversal, and that the zeroes of ![]() have no accumulation
point on the
have no accumulation
point on the ![]() -axis. Then it follows that generically
pathological cases do not occur
[Str01a].
In all those
degenerate
cases with
-axis. Then it follows that generically
pathological cases do not occur
[Str01a].
In all those
degenerate
cases with ![]() or
or ![]() for some
for some ![]() , an arbitrarily small variation of
either
, an arbitrarily small variation of
either ![]() or
or ![]() should suffice to eliminate the pathological
situation.
The disadvantage of this argument, though, is its heuristic nature, due
to the lack of an explicit, integrated formula for the
should suffice to eliminate the pathological
situation.
The disadvantage of this argument, though, is its heuristic nature, due
to the lack of an explicit, integrated formula for the ![]() .
.
ANDERSON localization of the kicked harmonic oscillator appears to be
a quite
general,
and perhaps even generic phenomenon:
in the preceding subsections,
I have motivated the fact that
the most important ingredients of all transfer matrices are the diagonal
energies (5.81) which are independent of the
kick potential. Only the period ![]() of the kicks enters equation
(5.81)
in a truly significant way.
The matrix elements (5.83), on the other hand, have
been seen to be rather irrelevant for the localization properties
-- as long as they give rise to tight or at least narrow binding --
and the matrix elements
mark
the
only
point where properties of the kick potential enter
the theory. What is more, in the matrix elements the kick potential
effectively gets randomized by being used as the argument of the
tangent only -- cf. equation (5.75).
In this sense, quantum localization of the
nonresonant
kicked harmonic oscillator
should be expected for generic kick functions, not only for the
cosine kick potential (1.18).
With respect to the value of
of the kicks enters equation
(5.81)
in a truly significant way.
The matrix elements (5.83), on the other hand, have
been seen to be rather irrelevant for the localization properties
-- as long as they give rise to tight or at least narrow binding --
and the matrix elements
mark
the
only
point where properties of the kick potential enter
the theory. What is more, in the matrix elements the kick potential
effectively gets randomized by being used as the argument of the
tangent only -- cf. equation (5.75).
In this sense, quantum localization of the
nonresonant
kicked harmonic oscillator
should be expected for generic kick functions, not only for the
cosine kick potential (1.18).
With respect to the value of ![]() , one may also speak of genericity of
localization in
an additional sense: under variation of
, one may also speak of genericity of
localization in
an additional sense: under variation of ![]() , the resonant values
(5.85) not
leading to ANDERSON localization are
obtained with probability zero.
, the resonant values
(5.85) not
leading to ANDERSON localization are
obtained with probability zero.
It is interesting to note the fundamental difference between the
conditions of nonresonance that lead to quantum localization in the
two model systems considered in this chapter:
The resonance condition (5.67) for the quantum
kicked rotor is obviously a consequence of the quantum nature of
the system, as the expression (5.67)
involves the PLANCK constant ![]() and has no classical counterpart.
On the other hand, nonresonance in the context even of the quantum
version of the kicked harmonic oscillator involves just the classical
resonance condition (1.22) on the kick period
and has no classical counterpart.
On the other hand, nonresonance in the context even of the quantum
version of the kicked harmonic oscillator involves just the classical
resonance condition (1.22) on the kick period
![]() .
It is one of the advantages of the particular scaling
(1.15, 1.16, 2.4)
of the dynamical variables and parameters employed here, that it
clearly exposes this property of the dynamics, in contrast to the scaling
used elsewhere [BRZ91].
So, using the abovementioned scaling, quantum localization in the kicked
harmonic oscillator comes about as
a genuine quantum phenomenon
-- without a classical analogue --
that is entirely controlled by a classical parameter:
the question of
nonresonance of the kick period
.
It is one of the advantages of the particular scaling
(1.15, 1.16, 2.4)
of the dynamical variables and parameters employed here, that it
clearly exposes this property of the dynamics, in contrast to the scaling
used elsewhere [BRZ91].
So, using the abovementioned scaling, quantum localization in the kicked
harmonic oscillator comes about as
a genuine quantum phenomenon
-- without a classical analogue --
that is entirely controlled by a classical parameter:
the question of
nonresonance of the kick period ![]() alone
decides on the localization of quantum states in the kicked harmonic
oscillator.
In particular, the existence of localization is independent of the strength
of the kicks.
Then, the other parameters
alone
decides on the localization of quantum states in the kicked harmonic
oscillator.
In particular, the existence of localization is independent of the strength
of the kicks.
Then, the other parameters ![]() and
and ![]() , via the matrix elements
(5.86), control the strength of the interaction between
the ``sites'' and determine if there is -- approximately -- tight
binding or rather some medium range interaction; in the same way they
control the localization length of the system.
, via the matrix elements
(5.86), control the strength of the interaction between
the ``sites'' and determine if there is -- approximately -- tight
binding or rather some medium range interaction; in the same way they
control the localization length of the system.
A final remark on the numerical results in section
5.2 and
section C.4 of the appendix:
for some of the presented examples,
the quantum map has been iterated for a very large number of times.
Up to and beyond ![]() kicks have been considered, while the number of
harmonic oscillator eigenfunctions taken into account for the basis was
only between 3000 and 6000.
This was possible just because of the quantum localization of the
systems considered in that and the present section; otherwise, for example
for the resonant systems discussed in chapter
4, such basis sizes would have allowed kick
numbers only typically not exceeding a few thousand.
kicks have been considered, while the number of
harmonic oscillator eigenfunctions taken into account for the basis was
only between 3000 and 6000.
This was possible just because of the quantum localization of the
systems considered in that and the present section; otherwise, for example
for the resonant systems discussed in chapter
4, such basis sizes would have allowed kick
numbers only typically not exceeding a few thousand.