Having discussed
the properties of the FLOQUET operator from a
general point of view, I now proceed to the
investigation
of the specific
![]() defined by
equations (2.8) and (2.14)
with the Hamiltonian
(2.5) of the kicked harmonic oscillator.
defined by
equations (2.8) and (2.14)
with the Hamiltonian
(2.5) of the kicked harmonic oscillator.
As its classical counterpart
![]() in equations
(1.20),
in equations
(1.20),
![]() can be decomposed into a contribution
can be decomposed into a contribution
![]() , describing the kick, and the propagator of the free
harmonic
oscillator dynamics for time
, describing the kick, and the propagator of the free
harmonic
oscillator dynamics for time ![]() ,
,
![]() :
:
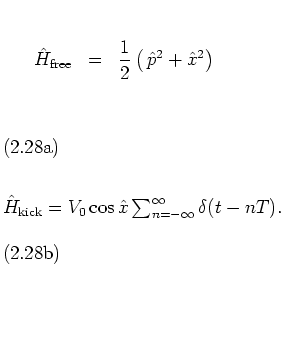
The free propagator -- as many more expressions to follow -- is most
conveniently expressed in terms of the ladder operators
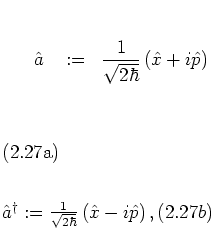
which can be used to write
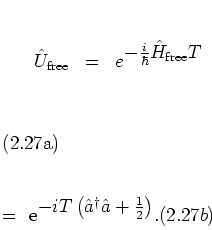
The computation of the kick propagator requires slightly more effort
because of the explicit time-dependence of the kick part of the
Hamiltonian.
Dividing the SCHRÖDINGER equation in coordinate representation by the
corresponding wave function
![]() , and
integrating over time at the
, and
integrating over time at the ![]() -th kick I
-th kick I
obtain
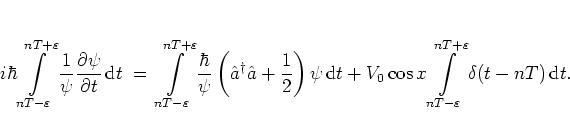 |
(2.27) |
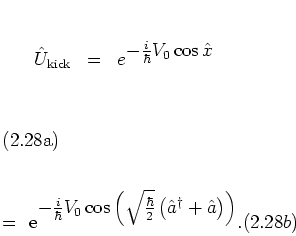
Summarizing,
this gives for the full FLOQUET operator
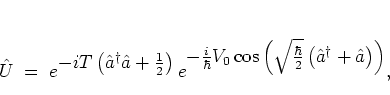 |
(2.28) |
Note that equation (2.37) cannot be simplified
significantly by restricting the discussion to values of ![]() that
satisfy a resonance condition (1.23) as in the
classical case (cf. equations
(1.25-1.29)).
This statement also holds with respect to the explicit expressions for
the matrix elements of
that
satisfy a resonance condition (1.23) as in the
classical case (cf. equations
(1.25-1.29)).
This statement also holds with respect to the explicit expressions for
the matrix elements of ![]() that I derive in subsection
2.1.3; there,
that I derive in subsection
2.1.3; there, ![]() may take any value as well.
For the comparison of classical and quantum results
on stochastic webs,
one has to concentrate on resonant values of
may take any value as well.
For the comparison of classical and quantum results
on stochastic webs,
one has to concentrate on resonant values of ![]() .
The
way in which the choice of
.
The
way in which the choice of ![]() controls the
existence of quantum mechanical periodic stochastic webs
is
discussed
in chapter 4;
for the discussion of ANDERSON localization in
chapter 5,
nonresonant values of
controls the
existence of quantum mechanical periodic stochastic webs
is
discussed
in chapter 4;
for the discussion of ANDERSON localization in
chapter 5,
nonresonant values of ![]() are in the focus of attention.
are in the focus of attention.