Introduction

In this paper we describe a generalization of a very powerful tool for the analysis of Hamiltonian dynamical systems: the theory of normal forms. Originally developed by Birkhoff in 1927 [1] who considered only nonresonant systems near an equilibrium point, the theory was brought into its classical form by Gustavson [2] who showed how to normalize¹even in the presence of resonant frequencies. Later important contributions were made by Bryuno [3]. The Birkhoff-Gustavson normal form (BGNF) has received considerable attention because of its utility in finding approximate constants of motion [4,5,6,7,8] and quantizing nonlinear Hamiltonian systems [9,10,11,12,13].

The key idea of the theory is to systematically perform a series of canonical transformations, thus bringing the Hamiltonian into a particularly simple form, its ``normal form''. In this context simplicity means the possibility to read off an expression for a second integral of motion directly from the normal form Hamiltonian. More precisely, for a Hamiltonian $H$ in BGNF the quadratic part of $H$ is proven to be an integral of motion.

Gustavson considered an autonomous Hamiltonian system of $n$ degrees of freedom in the vicinity of a stable equilibrium point, such that in lowest order approximation the Hamiltonian can be written as an $n$-dimensional harmonic oscillator, while the anharmonic parts of the system are given by a power series of order 3 and higher in the coordinates ${\mbox{\protect\boldmath$q$}}\in{\bf R}^n$ and the momenta ${\mbox{\protect\boldmath$p$}}\in{\bf R}^n$:

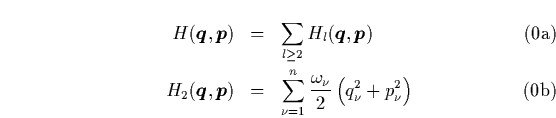
with real frequencies $\omega_\nu>0$ and $H_l$ being a homogoneous polynomial of degree $l$ in $q_\nu$ and $p_\nu$. Gustavson's theory necessarily requires the quadratic part of $H$ to be of the particular form (1b). Only for this special $H_2$ he can define his normal form, prove normalizability and show how to obtain (an asymptotic expression for) a second invariant. In section 2.1 of this paper we will show in detail how this restriction comes about.

Several attempts have been made to approach the problem from a more general point of view, making it possible to normalize not only Hamiltonians of the Gustavson type [14,15,16,17,18]. However, until recently there has been no general method that could be applied to Hamiltonians with an arbitrary $H_2$ term. It is this problem that we will address and exemplify in the following sections. Similar (and more general) results have been obtained by Meyer and Hall in [19], though their approach -- and especially their proof of what corresponds to our main theorem (cf. section 2.3) -- is quite different from ours. It is our goal to give a more easily readable account of the theory and to demonstrate in some detail the practical application to a given Hamiltonian and the calculation of the quasi-integral.

In section 2 we formulate the normalization process in terms of Lie operators and Lie transformations and use these techniques to develop a generalized approach, suitable for any $H_2\not\equiv 0$. Section 3 is dedicated to the application of the generalized normal form to a model system that cannot be analyzed by means of the Birkhoff-Gustavson theory. As the model system we have chosen a particular type of magnetic bottle that can be used as an ion trap in laboratory experiments. Our main result from the normal form calculations is the derivation of an expression for a formal integral of motion $I$ up to and including the 14th order. The convergence properties of this quasi-integral are analyzed in section 3.2; $I$ exhibits a surprisingly rich structure and can be used to reproduce reasonably well the corresponding Poincaré plot.

Footnotes

... normalize¹

Throughout this paper, the term ``normalization'' refers to the process of
transforming a Hamiltonian into its normal form. This is not to be confused with, say, the
normalization of a vector.