On the power of normal form theory:

Simplification of a Hamiltonian dynamical system
using normal form theory and quasiintegrals of motion

by Martin Engel

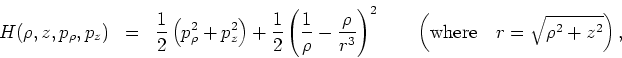
Consider the well-known Størmer problem which is given by the Hamiltonian

$$\begin{eqnarray*} H(\rho,z,p_\rho,p_z) & = & \frac{1}{2}\left(p_\rho^2+p_z^2\ri... ...ft(\mbox{\normalsize where} \quad r = \sqrt{\rho^2+z^2}\right), \end{eqnarray*}$$

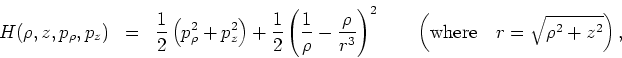
completely describing the classical motion of a charged particle in the earth's magnetic field (which is assumed here to be a pure dipole field).

As the first step of our simplification procedure, we transform from the ordinary cylindrical polar coordinates $(\rho,\varphi\hspace*{-0.3cm}\times,z)$ used above to dipolar coordinates $(a,b)$ and expand the resulting expression in terms of these new coordinates and their corresponding canonically conjugate momenta $p_a$, $p_b$ (cf. G. Contopoulos, L. Vlahos, J. Math. Phys. 16 (1975) 1469-1474):

$$\begin{eqnarray*} H(a,b,p_a,p_b) & = & %**************************************... ...************************************************ + {\cal O}(13) \end{eqnarray*}$$

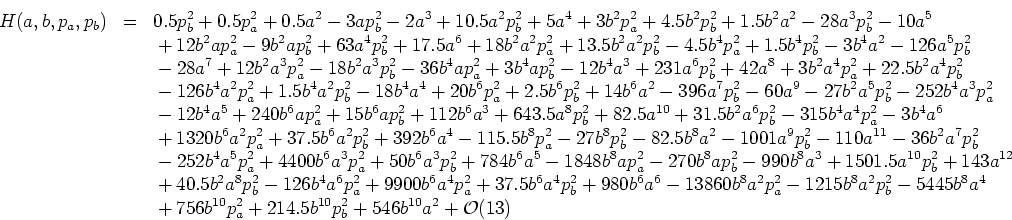
Now generalized normal form theory (U. M. Engel, B. Stegemerten, P. Eckelt, J. Phys. A: Math. Gen. 28 (1995) 1425-1448) can be applied to this transformed Hamiltonian, yielding the following most simple normal form for the Størmer problem:

$$\begin{eqnarray*} G(a,b,p_a,p_b) & = & %**************************************... ...************************************************ + {\cal O}(13) \end{eqnarray*}$$

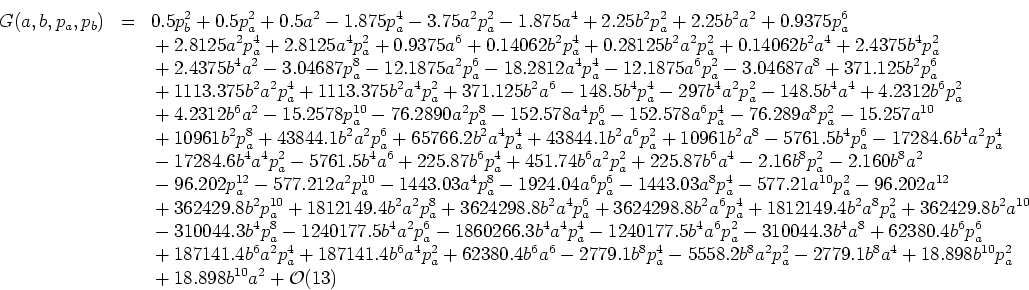
The third, and final, step on our path towards maximum simplicity is the transformation of the above normal form into the corresponding quasiintegral of motion; for our little sample problem, a minute's thought will reveal that we have:

$$\begin{eqnarray*} I(a,b,p_a,p_b) & = & %**************************************... ...6 p_b p_a +9417.975 b^2 a p_a^6 +292971.191 b^2 a p_b^2 p_a^4 \end{eqnarray*}$$

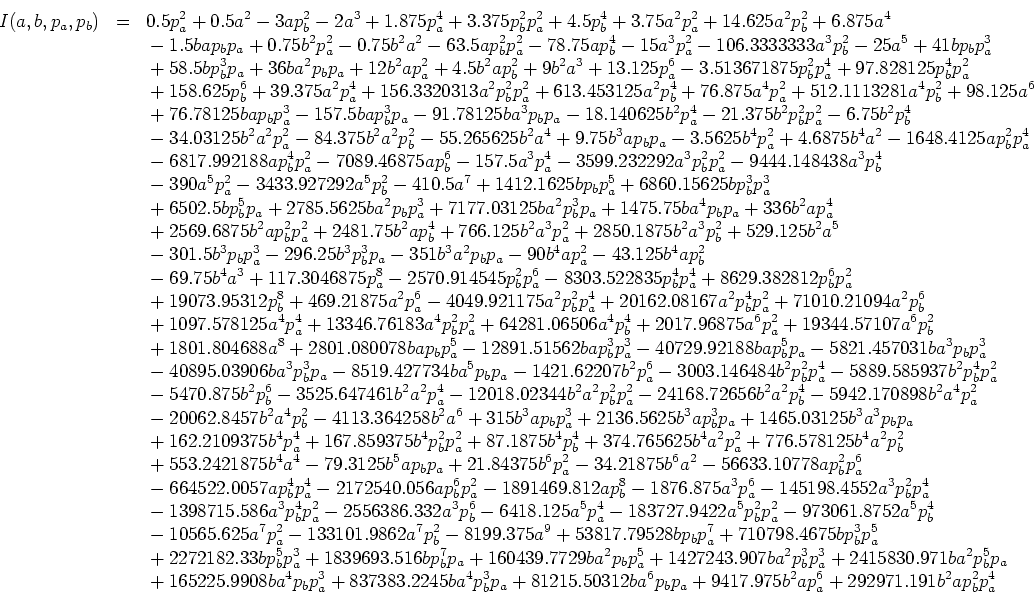
$$\begin{eqnarray*} {}\mbox{{}\rule{2.6cm}{0.0001cm}{}}{} %ME &&{} +988776.6406... ...b^3 p_b^5 p_a^3 -109960281.2 b^3 p_b^7 p_a %ME \\ [-0.1cm]&&{} \end{eqnarray*}$$

$$\begin{eqnarray*}%ME {}\mbox{{}\rule{2.6cm}{0.0001cm}{}}{} %ME &&{} -14084153... ...*********************************************** + {\cal O}(13) \end{eqnarray*}$$

The most impressive simple structure of this tiny little formula and its evident meaningfulness immediately show the superiority of our simplification algorithm.