| It is the nature of all greatness not to be exact. | ||
| EDMUND BURKE |
Using
measure theoretical methods,
FURSTENBERG
has derived a theorem that is
useful
for proving ANDERSON
localization
on
one-dimensional lattices as,
for example,
in chapter 5
of this
study.
The theorem deals with a specific class of random matrices
![]() ,
,
![]() ,
and states that generically the norms of the vectors
,
and states that generically the norms of the vectors
![]() tend to
infinity
at an exponential rate with
tend to
infinity
at an exponential rate with ![]() ,
provided
that
certain
-- not very restrictive
--
conditions
are met.
The theorem is
applied
in chapter 5,
where the role of the
,
provided
that
certain
-- not very restrictive
--
conditions
are met.
The theorem is
applied
in chapter 5,
where the role of the ![]() is taken by the transfer matrices
is taken by the transfer matrices ![]() .
.
Consider the classical group
![]() of unimodular real
of unimodular real
![]() matrices
with the usual matrix product.
A subgroup
matrices
with the usual matrix product.
A subgroup ![]() of
of
![]() is called irreducible if the only
subspaces of
is called irreducible if the only
subspaces of ![]() left fixed by the matrices
of
left fixed by the matrices
of ![]() are
are ![]() and
and
![]() ; otherwise
; otherwise ![]() is
called reducible.
Let
is
called reducible.
Let ![]() be a measure on
be a measure on
![]() ,
induced by
the distribution of the elements
of a given set of unimodular matrices
,
induced by
the distribution of the elements
of a given set of unimodular matrices
![]() ,
and let
,
and let ![]() be the smallest closed
subgroup of
be the smallest closed
subgroup of
![]() that contains the support of
that contains the support of ![]() .
.
FURSTENBERG's theorem discloses some details of the asymptotic behaviour
of the norms
![]() of the vectors
of the vectors
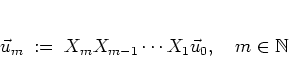 |
(B.1) |
Theorem.
If ![]() is irreducible and
is irreducible and ![]() satisfies
satisfies
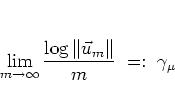 |
(B.3) |
The theorem holds with probability one only, due to the random nature of
the ![]() . Almost all such sequences of matrices
-- and thus almost all distributions of matrices obtained in this way --
give the desired result,
but there are some that do not. The probability of
coming by such an exceptional case
is zero, though, such that for all practical applications the
theorem can be considered to be true.
The (rather technical) proof of
the
theorem is given in FURSTENBERG's
paper [Fur63].
. Almost all such sequences of matrices
-- and thus almost all distributions of matrices obtained in this way --
give the desired result,
but there are some that do not. The probability of
coming by such an exceptional case
is zero, though, such that for all practical applications the
theorem can be considered to be true.
The (rather technical) proof of
the
theorem is given in FURSTENBERG's
paper [Fur63].
In a typical application
one is given a set
![]() of unimodular matrices with a
distribution
of unimodular matrices with a
distribution ![]() on
on
![]() . First one has to
identify the corresponding matrix group
. First one has to
identify the corresponding matrix group ![]() ; then irreducibility and
noncompactness of
; then irreducibility and
noncompactness of ![]() need to be confirmed.
This, by FURSTENBERG's theorem,
establishes the result
that for almost all such sets
need to be confirmed.
This, by FURSTENBERG's theorem,
establishes the result
that for almost all such sets
![]() with a
sufficiently well-behaved
measure
with a
sufficiently well-behaved
measure ![]() ,
the norms of the vectors
,
the norms of the vectors ![]() grow exponentially
for large
grow exponentially
for large ![]() ,
,
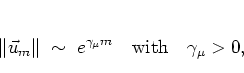 |
(B.4) |
For ![]() , the most important example is
, the most important example is
![]() itself:
itself:
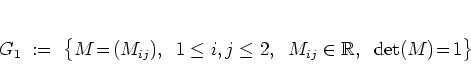 |
(B.5) |
The group given by
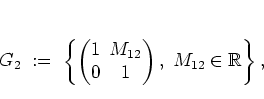 |
(B.7) |
For ![]() , the theorem is used in
subsection 5.3.3
with respect to
, the theorem is used in
subsection 5.3.3
with respect to
![]() itself:
the transfer matrices
(5.123a) and (5.124a)
belong to the group defined by
itself:
the transfer matrices
(5.123a) and (5.124a)
belong to the group defined by
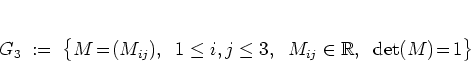 |
(B.8) |